88 | CONCRETO & Construções | Ed. 88 | Out– Dez • 2017
de carga às quais estará submetido
um anel segmentado, apresentadas na
figura 1, podem ser as mais desfavo-
ráveis no dimensionamento, pois po-
dem conduzir aos esforços de flexão
de maior magnitude que os atuantes
durante o uso do elemento. Mesmo
assim, devido às dimensões da seção
transversal dos segmentos e por en-
volver apenas as ações do peso pró-
prio (amplificado por efeitos dinâmicos,
em alguns casos), as necessidades de
reforço são reduzidas, o que deman-
da quantidades mínimas de armadu-
ra para atingir os níveis de segurança
adequados. Adicionalmente, se devem
considerar ações climáticas nas situa-
ções de estocagem, as quais podem
provocar fortes gradientes de deforma-
ção e, consequentemente, tensões de
tração e fissuras (não estruturais) nas
faces externas dos segmentos. Para
essas situações, as fibras proporcio-
nam uma melhor resposta que as ar-
maduras convencionais por controlar a
abertura de fissura em todo o volume
do segmento.
2.2 Critérios para substituir
as barras da armação por
fibras estruturais
Os seguintes critérios podem ser
considerados para confirmar o poten-
cial de substituição das barras por fi-
bras estruturais:
u
Análise seccional e/ou estrutural
considerando as equações cons-
titutivas propostas no
fib
Model
Code 2010 (FIB, 2013) para simu-
lar o comportamento
σ
–
ε
do CRF
– para este tipo de análise se em-
pregam valores característicos das
resistências dos materiais;
u
Ensaios em escala real de elementos
submetidos à flexão com as dimen-
sões representativas do segmento
objeto de análise.
2.3 Procedimento de projeto
segundo a consideração de
segurança dos estados limite
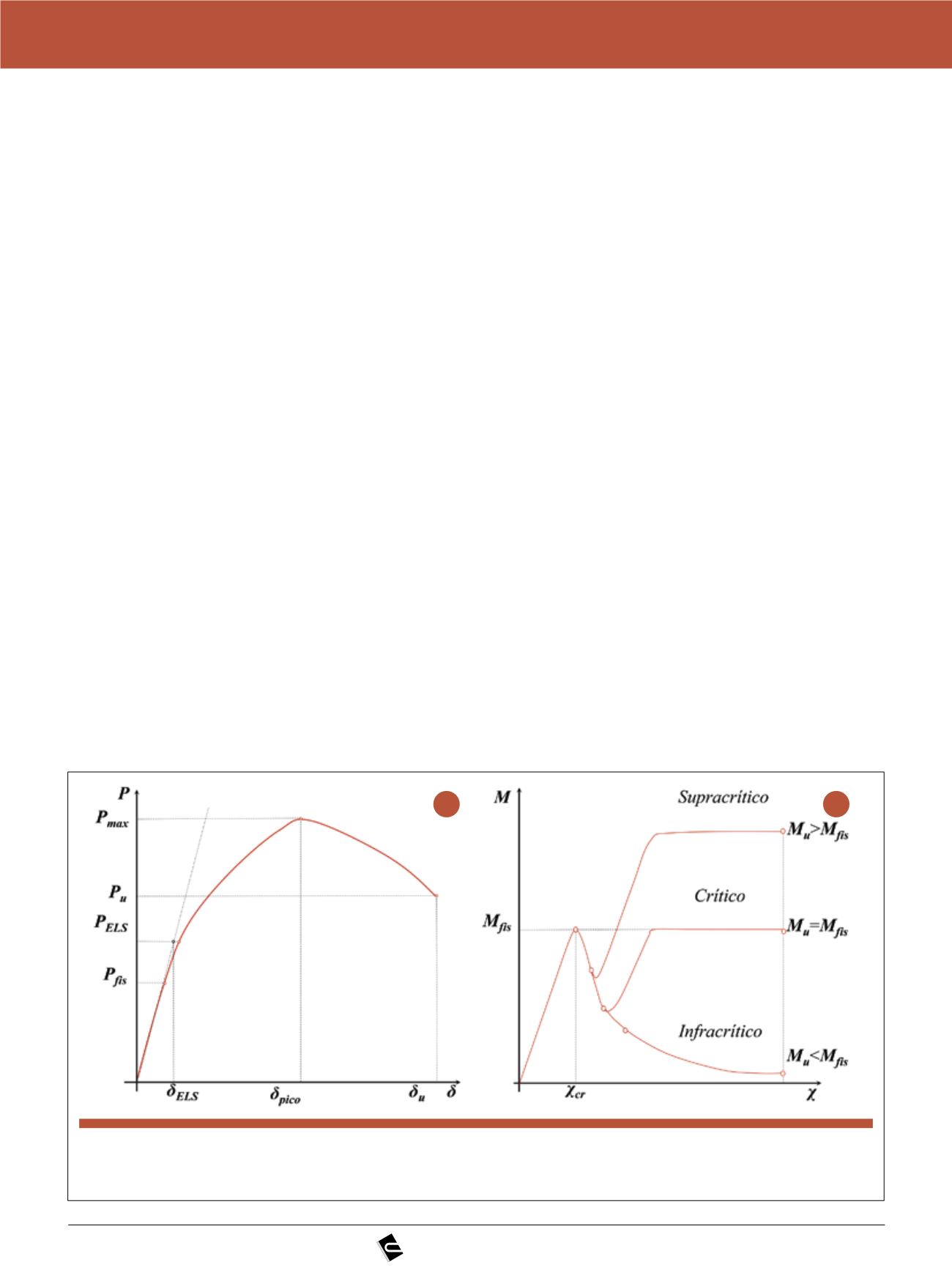
No caso de se empregar somen-
te fibras, o fib Model Code 2010 (FIB,
2013) estabelece três requisitos basea-
dos na curva de carga (P) por desloca-
mento (
δ
) apresentada na figura 5:
1) A carga última (P
u
) deve ser superior
à de fissuração (P
fis
) e à de serviço
(P
ELS
).
2) O deslocamento para P
u
(
δ
u
) deve
ser superior ao correspondente ao
ELS (
δ
ELS
).
3) O deslocamento para o ELS (
δ
ELS
)
deve ser ao menos 5 vezes inferior
ao deslocamento de pico (
δ
pico
) as-
sociado à carga máxima (P
max
).
O requisito 1 foi postulado para
evitar a ruptura frágil do elemento
quando se atinge a fissuração. Este
requisito, em elementos isostáticos,
também pode ser expresso em ter-
mos de momentos, como M
u
≥ M
fis
(momento último e de fissuração,
respectivamente). A relação P
fis
≥
P
ELS
(M
fis
≥ M
ELS
) pode ser imposta no
projeto dos segmentos (sem fissura-
ção em qualquer das fases transitó-
rias e de serviço); portanto, o requi-
sito 2 se cumpre por consequência
u
Figura 5
(a) curvas P-
δ
e (b) diagrama M-
χ
para elementos de CRF com diferentes volumes de fibra
b
a


