112 | CONCRETO & Construções
O valor da curvatura limite
f
0
(s,t)
pode ser considerado como a cur-
vatura no estado limite último da
seção, a curvatura máxima medida
durante uma prova de carga para
uma determinada seção ou, até
mesmo, a curvatura máxima obtida
através de simulação numérica uti-
lizando os carregamentos aciden-
tais de norma cabíveis. Para mais
considerações sobre a definição da
resposta limite considerada nesta
equação o leitor pode referir-se a
LIU et al. (2009).
Quando a avaliação da seguran-
ça estrutural utilizando a eq. 1 é feita
no instante t=0 (presente momento
da medição), os valores de
f
(s,t) po-
dem ser utilizados diretamente na
análise, ou seja,
z
(s,t)=1,0. Para es-
timar a segurança no futuro, os valo-
res de deformação podem se ajusta-
dos utilizando a função de previsão,
z
(s,t). LIU et al. (2009) propõem uma
função baseada na estatística de va-
lores extremos. Esta proposta se ba-
seia no fato de que, para um número
de medições
k
grande o suficiente,
a distribuição de valores extremos
(máximo ou mínimos) tende a umas
das três distribuições de probabili-
dade: (1) Gumbel; (2) Fisher-Tippett;
(3) Weibull, independentemente da
distribuição de probabilidades da
variável original.
A função de previsão proposta no
trabalho de Liu et al. é baseada na
distribuição de Gumbel, que apre-
senta a seguinte expressão para a
função de probabilidade cumulativa:
[2]
Onde, F(
f
m
) é a função cumulati-
va de distribuição que é a probabi-
lidade de ocorrência de um valor
f
menor ou igual a
f
m
(F(
f
m
) = P[
f ≤ f
m
,
f
m
é o valor extremo da variável ale-
atória
f
e
l
e
h
são os parâmetros
da distribuição, que podem ser ob-
tidos através dos dados de medi-
ção utilizando métodos estatísticos
(ANG; TANG, 2007).
Desta forma, o valor máximo
dos dados medidos nos próximos
T anos,
f
max
(T), pode ser estimado
invertendo-se a eq. 2 no seguinte
formato:
[3]
Sendo
f
max
(T) o maior valor em
N
T
ocorrências futuras, F(
f
max
(T)) é
dado por:
[4]
Onde,
N
T
é o número total espe-
rado de passagens de veículos pe-
sados sobre a ponte nos próximos
T
anos.
Desta forma inserindo a eq. 4 na
eq. 3, é obtida a expressão:
[5]
Assim, conforme apresentado por
LIU et al. (2009), a função de previsão
pode ser escrita de acordo com a eq. 6.
[6]
3. APLICAÇÃO EM UMA PONTE
DE CONCRETO ARMADO
3.1 Descrição da obra de arte
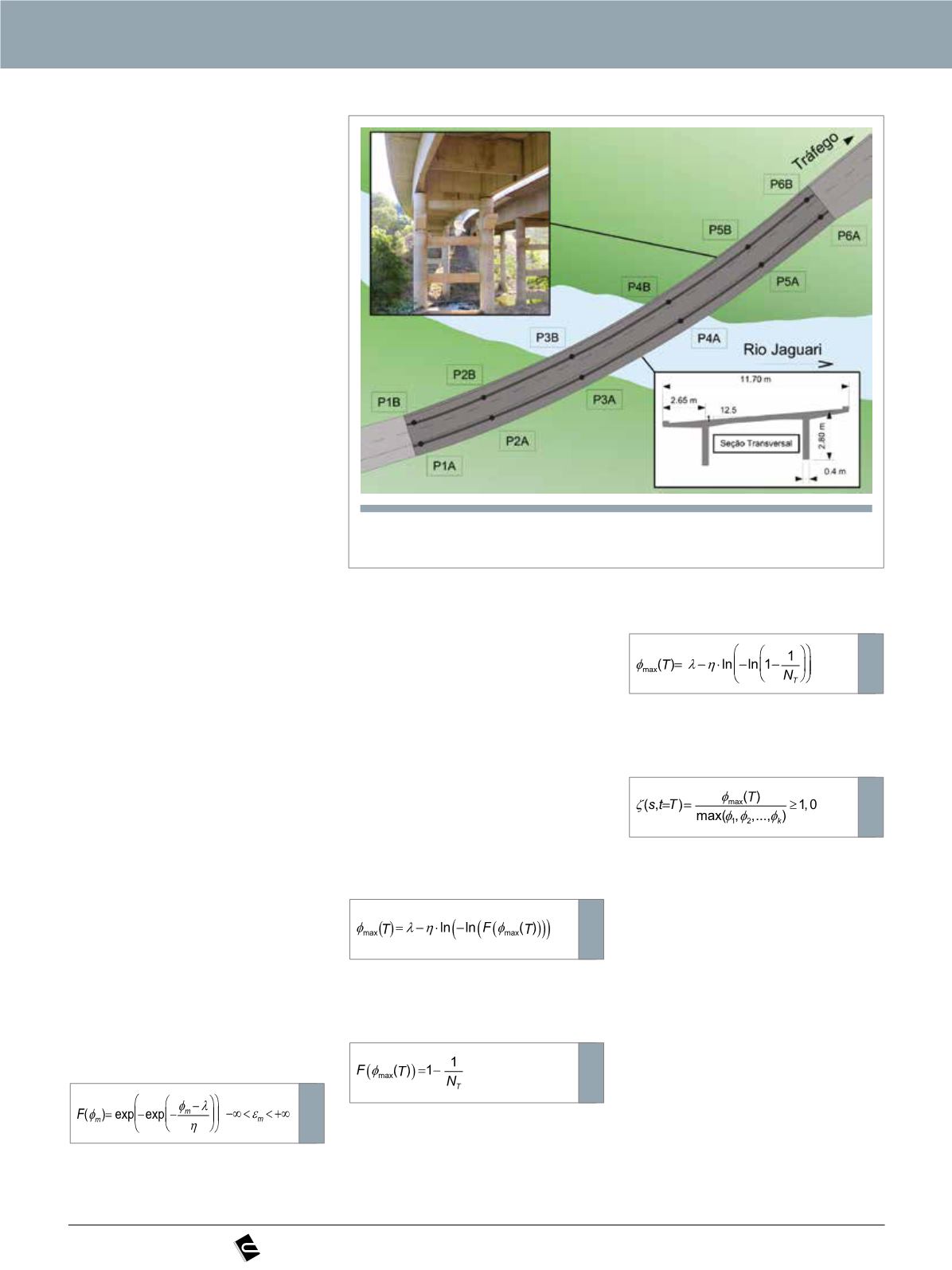
A ponte sobre o rio Jaguari (Figu-
ra 1), localizada no km 946+300 da
BR-381, no município de Extre-
ma (MG) sob concessão da Auto-
pista Fernão Dias, foi seleciona-
da para ter seu comportamento
estrutural estudado por meio do
monitoramento das deformações,
deslocamentos e acelerações. A
u
Figura 1
Ponte sobre o rio Jaguari


