CONCRETO & Construções | 115
é a variação máxima da curvatura
devido às cargas acidentais de nor-
ma sobre a mesma.
Com esses valores de curvatura
limite é possível calcular a probabi-
lidade de falha associada a eq. (1).
Foi empregado para este fim o mé-
todo FORM (MELCHERS, 1999) e os
resultados obtidos encontram-se na
Tabela 2. Nos campos da tabela que
se encontram em branco, as proba-
bilidades de falha foram menores do
que a precisão obtida com a plata-
forma de cálculo utilizada.
4.
CONSIDERAÇÕES FINAIS
Neste trabalho foi apresentada
uma metodologia para a avaliação da
segurança estrutural de uma ponte
em concreto armado utilizando dados
de monitoramento estrutural. Dados
coletados durante uma empreitada de
monitoramento foram empregados e
a partir deles foram obtidas algumas
distribuições probabilísticas. Através
do uso de diagramas de momento x
curvatura para as seções de concre-
to armado e de um modelo analítico
linear para a estrutura da ponte, fo-
ram obtidos valores de curvatura li-
mite. Utilizando esses valores limites,
foram calculadas probabilidades de
falha associados a eles. A formulação
apresentada é de fácil implementação
e, quando modelada adequadamen-
te, permite acompanhar o desempe-
nho estrutural da ponte quanto ao seu
comportamento à flexão.
A interpretação dos valores de
probabilidade apresentados na Ta-
bela 2 deve ser feito de acordo
com a definição do valor de cur-
vatura limite. Por exemplo, caso a
curvatura limite seja estabelecida
com base na capacidade última da
u
Tabela 1 – Parâmetros das distribuições ajustados para os dados de medição
Seção
Fisher-Tippett (GEV)
Weibull
k
s
(x10
-6
)
m
(x10
-6
)
l
(x10
-6
)
k
S1-A
0,015978
9,34753
17,8406
–
–
S1-B
–
–
–
3,02687
1,69307
S3-A
0,307376
4,47532
8,30104
–
–
S3-B
–
–
–
1,07235
2,09033
S5-A
0,153226
3,80527
6,54558
–
–
S5-B
–
–
–
1,08796
1,80363
u
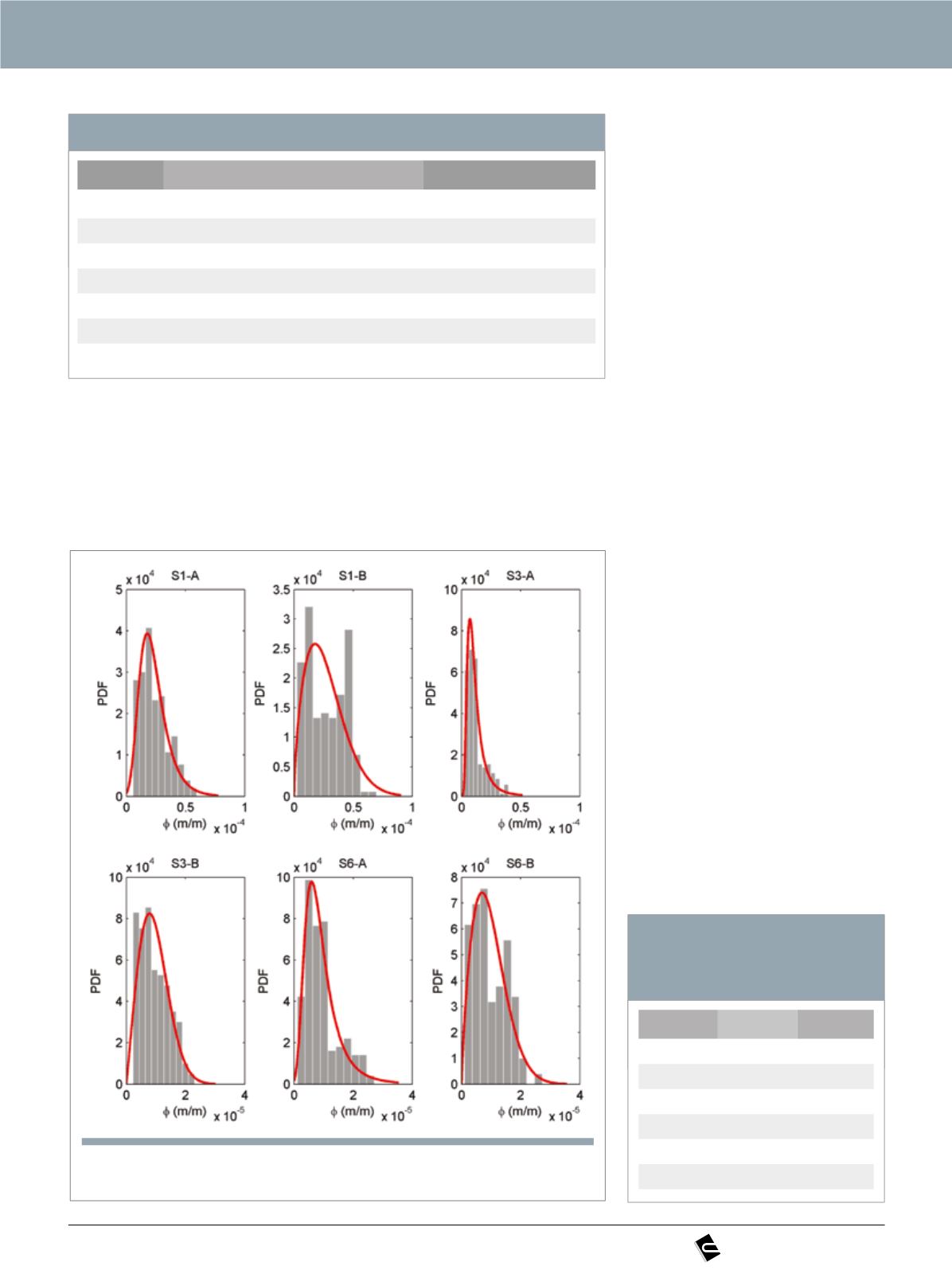
Figura 6
Funções de densidade de probabilidade obtidas para os dados de curvatura
u
Tabela 2 – Parâmetros das
distribuições ajustados para
os dados de medição
Seção
f
0
(x 10
-5
)
P [ g
≤
0]
S1-A
13,204 1,57 x 10
-5
S1-B
13,421 5,37 x 10
-6
S3-A
8,2000 2,86 x 10
-3
S3-B
8,4000
–
S5-A
9,5321 5,01 x 10
-5
S5-B
9,6571
–


