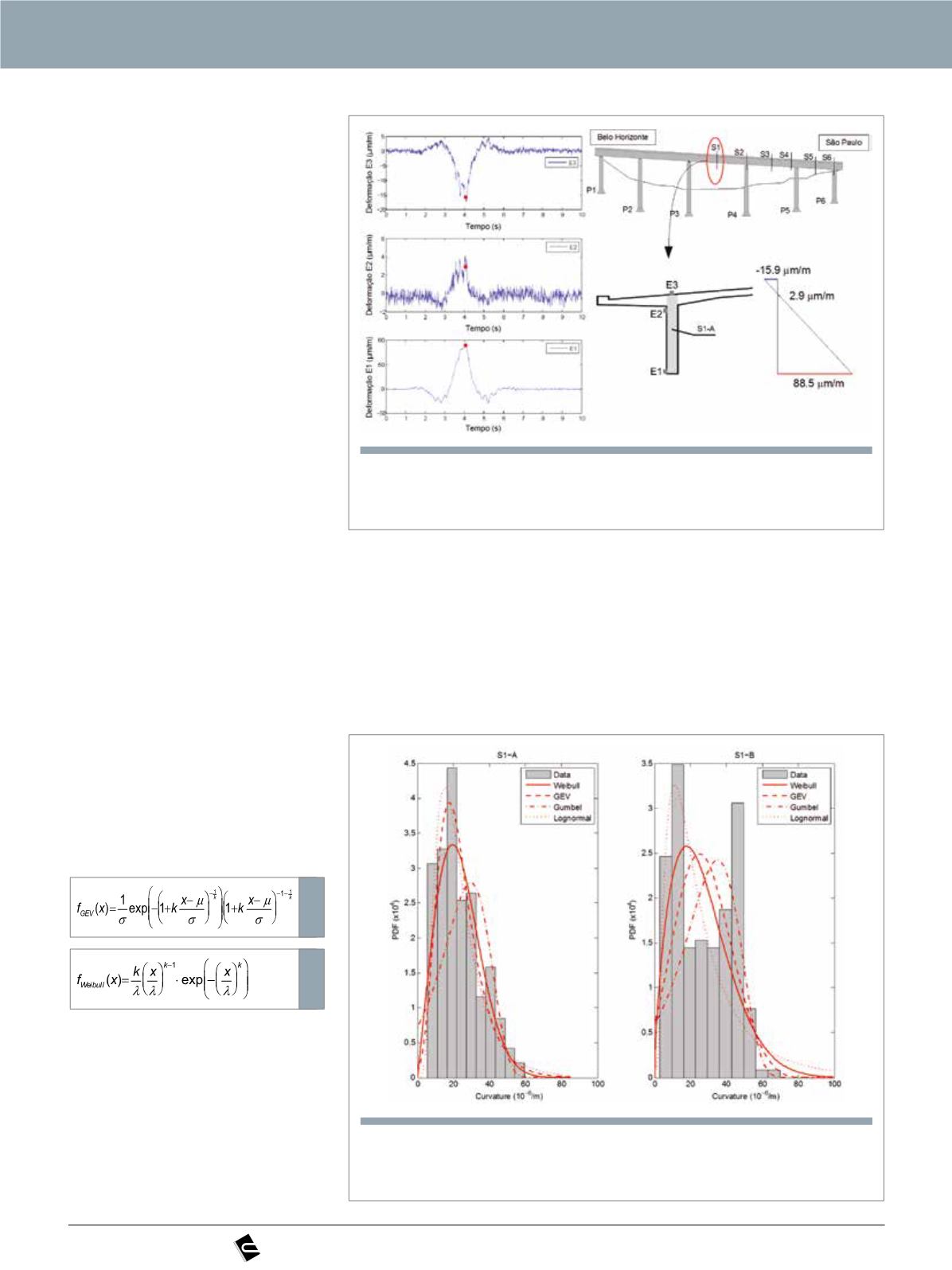
114 | CONCRETO & Construções
curvatura devidos às passagens de
veículos sobre a ponte. Utilizando a
ferramenta
MATLAB
®
e o método de
Maximum Likelihood
(ANG; TANG,
2007) foi possível ajustar os parâ-
metros das distribuições de Wei-
bull, Fisher-Tippett (GEV), Gumbel e
Lognormal para os dados obtidos. A
Figura 5 mostra o resultado desses
ajustes para cada uma destas distri-
buições para a seção S1-A e S1-B.
Analisando os resultados dos
ajustes da distribuições concluiu-
-se que, para as seções da viga A, a
distribuição de Fisher-Tippett (GEV)
é a mais adequada e, para as se-
ções da viga B, a distribuição de
Weibull se aproximou mais dos da-
dos medidos. A Tabela 1 mostra os
valores dos parâmetros encontra-
dos para cada uma das seções ana-
lisadas. Para melhor entendimento
dos parâmetros de cada distribui-
ção, as equações 8 e 9 mostram a
função de densidade de probabili-
dade (PDF) para as distribuições de
Fisher-Tippett e Weibull, respectiva-
mente. Na Figura 6 estão plotadas
as funções de densidade de pro-
babilidade (PDF) que apresentaram
melhor ajuste aos dados de campo
coletados.
[8]
[9]
3.3 Avaliação da segurança
utilizando os dados de
monitoramento
Utilizando os parâmetros das dis-
tribuições obtidos através dos dados
de monitoramento é possível calcular
a probabilidade de falha associada à
equação de estado limite estabeleci-
da pela eq. (1). Para isso, é neces-
sário determinar o valor de curvatura
limite a ser utilizado. Neste trabalho
este valor foi obtido através da apli-
cação das cargas de norma em um
modelo analítico. A metodologia para
estimar esta curvatura a partir da re-
lação momento x curvatura e do mo-
delo analítico da ponte está ilustrado
na Figura 7. Neste método é neces-
sário considerar o efeito das cargas
permanentes na seção e avaliar qual
u
Figura 4
Deformações durante a passagem de um veículo sobre a ponte e perfil das
deformações no ponto de deformação máxima para a seção S1-A
u
Figura 5
Funções de densidade de probabilidade ajustadas para os dados
de curvatura da seção S1


