CONCRETO & Construções | 35
nesse nó já se tem a força (compressão no concreto) igual a:
[14]
0,10 809,6 80,96
kN
´ =
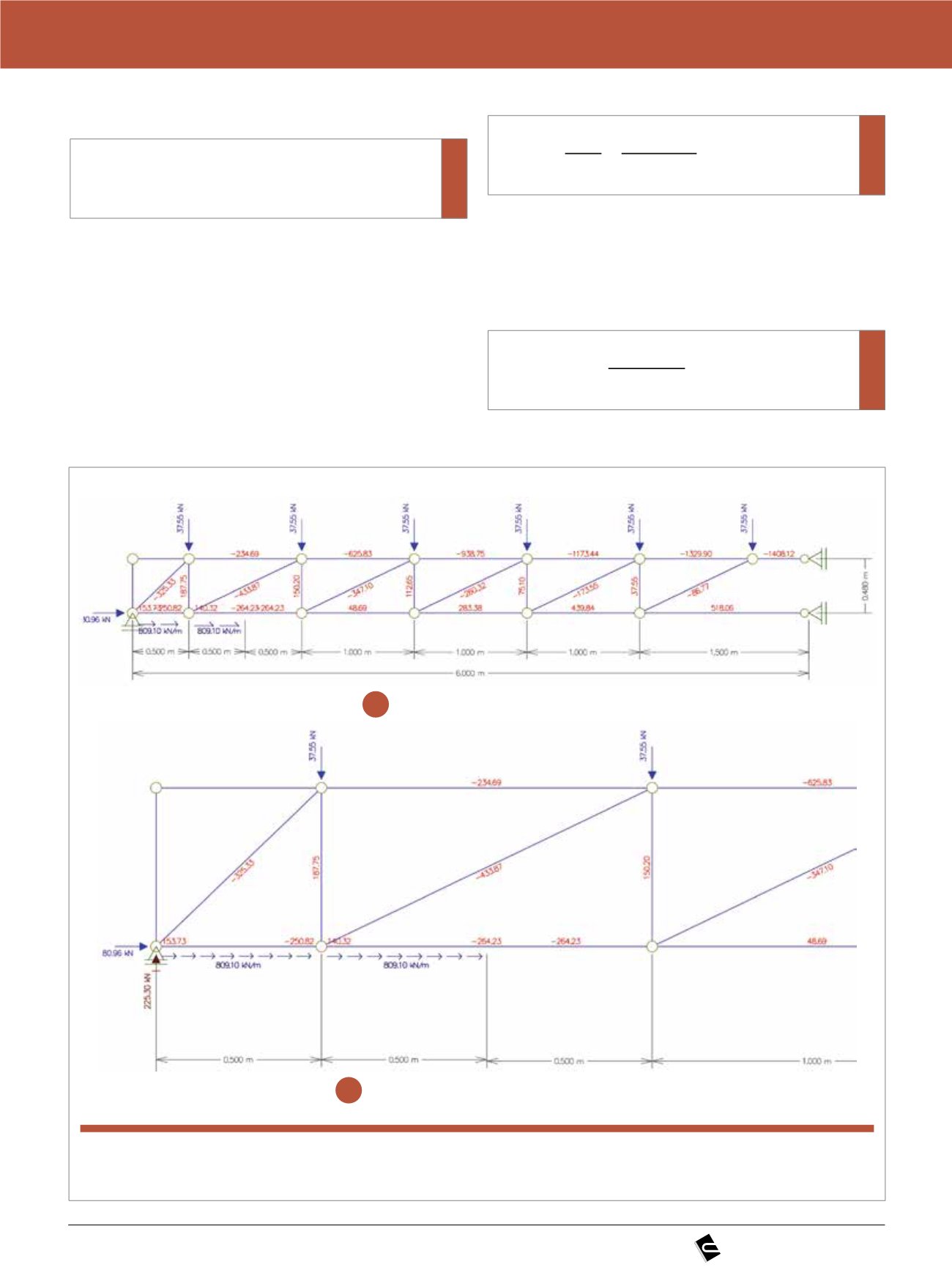
Com estes dados, resulta a treliça da Figura 3.
A Figura 3 mostra as forças nos banzos, nas diagonais
e nos montantes da alma em toda a viga. Assim, a arma-
dura protendida está sob a ação das forças distribuídas
,
nd
p
∞
(externas à armadura protendida) nos primeiros
1,1
m
(e em
1
m
nas barras da treliça), correspondentes à for-
ça interna constante e igual a
,
890
nd
P
kN
∞
=
nos restantes
(
)
12, 20 2 1,1 10, 0
m
− × =
. Esta força consome parte da resis-
tência do aço de protensão, igual a:
u
Figura 3
Treliça no plano vertical da alma da viga
Forças normais nas barras da treliça
a
Detalhe das forças normais na região do apoio
b
[15]
3
,
,
890 10 1059,5
Σ 2 3 140
nd
pnd
p
P
MPa
A
s
¥
¥
´
= =
=
´ ´
Como as forças na armadura protendida são autoequili-
bradas e não há reação de apoio pela ação da protensão em
peça isostática, ao aplicar as cargas, obtêm-se as forças no
banzo inferior (cf. a Figura 3), para as quais se tem à disposi-
ção a parcela complementar de resistência:
[16]
,
0,9 1900 1059,5 427,5
1,15
pyd
pnd
f
MPa
s
¥
´
- =
-
=
valor curiosamente próximo de
yd
f
do CA-50. Logo, o


