40 | CONCRETO & Construções
pré-tração baseada em tensões elásticas está indicada
no MC90, item 6.9.12. Por este caminho, neste exem-
plo não há fissuração na zona D e, mesmo que houves-
se, a armadura resultante não prevaleceria sobre a já
calculada.
2.3.5 M
ontagem
da
treliça
do
flange
e
dimensionamento
da
armadura
transversal
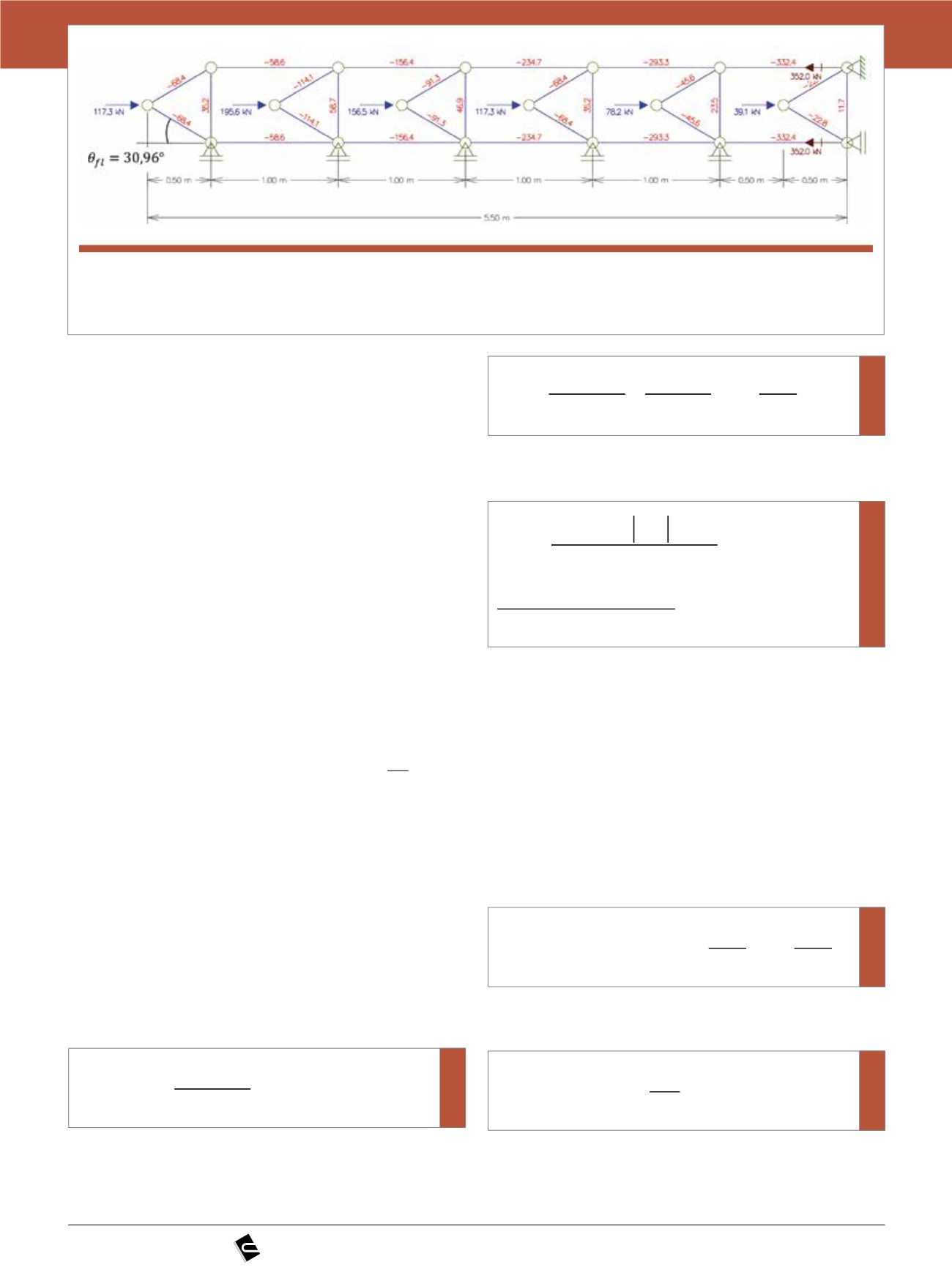
A Figura 7 mostra em planta a treliça corresponden-
te ao flange do
π
, (perpendicular à treliça da nervura),
considerando apenas meia largura, i.e.,
0,5 1, 20
fl
b
m
=
e
metade do vão, por causa da dupla simetria. Os apoios
contra translação horizontal distam cada qual
0,30
m
do
plano vertical da nervura.
Nota-se desde logo que a soma das forças aplica-
das é igual, no centro do vão, à força longitudinal de
compressão atuante em metade do flange
704
2
d
M kN
z
=
.
Assim, a força de compressão no centro do vão é trans-
ferida pouco a pouco para a alma da viga, até anular-
-se na extremidade do flange junto ao apoio. Em cada
nó superior da treliça vertical referente a uma nervura,
tem-se a força da diagonal (vinda do flange) multiplica-
da por
cos
θ
(e
a
cos
θ
no primeiro nó). Resultado igual
decorre da diferença das forças nodais horizontais.
Para obter a força de tração transversal
,
st fl
R
adota-
-se
30,96 ,
0, 6
fl
fl
tan
θ
θ
= °
=
(poderia ser
2 / 3
fl
tan
θ
=
,
cf. recomendado no item 9.6.2.2 e Figura 9.6 da NBR
6118:2014), donde seu valor máximo:
[39]
,
30,96
195, 6
195, 6 0,3 58,7
2
st fl
tan
R
kN
°
=
= ´ @
como indicado na Figura 7. Neste exemplo, mantém-se em
todo o flange a armadura calculada para esta máxima força,
a qual deve ser distribuída em
1
zcot
m
θ
=
:
u
Figura 7
Planta de metade do flange do , respectivas geometria e forças da treliça (Obs.: na barra vertical central dobrar a
p
força em virtude da simetria).
[40]
2
,
,
58,7 135
1 0,435
st fl
st fl
ywd
R
mm
a
zcot f
m
q
=
=
=
´
A compressão diagonal no concreto do flange é baixa, e
resulta da expressão:
[41]
(
)
,
,
(
)
c fl
c fl
fl
fl
max R
zcot
sen h
s
q
q
=
=
´
´
3
2
3
114,1 10
2,2
1 10
30, 96 100
cd
MPa f
sen
°
´
=
´ ´
´
=
Além desta armadura, deve-se considerar aquela necessária
para a flexão transversal do flange, o qual pode ser considera-
do como uma laje biapoiada nas nervuras sujeita a dois carre-
gamentos: (1) cargas totais em toda largura, para efeito da ar-
madura superior, e (2) peso próprio do flange mais o restante
da carga somente entre as nervuras. No exemplo bastam ar-
maduras transversais mínimas superior e inferior. Estas arma-
duras, cf. o item 17.3.5.2.1 da NBR 6118: 2014, para seção
retangular e
40
ck
f
MPa
=
, resultam da taxa geométrica míni-
ma,
0,18%
min
ρ
=
, referida à altura
h
do flange, donde:
[42]
2
2
,
0,18% 100 0,180
180
s min
mm mm
a
mm m
=
´ =
=
Assim, a armadura total transversal na camada superior do
flange é igual a:
[43]
2
, ,
135 180 315 1 8
15
,
stot fl
mm
a
cada cm superior
m
= + =
= Æ
E deve ser posicionada na face superior do flange, pois
na flexão do
π
resultou uma altura do bloco retangular de
tensões igual a
24, 4
100
fl
y
mm h
mm
=
=
. Longitudinalmente,


