CONCRETO & Construções | 45
momentos causados pelos trechos do
perímetro crítico, em relação ao eixo do pi-
lar em torno do qual atua o momento M
sd
.
[1]
ò=
1
0 1
.
u
dle
W
Onde:
“dl” é o comprimento elementar do pe-
rímetro de controle;
“e” é a distância de dl ao eixo em torno
do qual atua o momento M
sd
.
O fib MC 2010 recomenda, para la-
jes protendidas, que a carga F
sd
pode
ser reduzida pela soma das componen-
tes verticais das forças nas cordoalhas
passando pelo pilar ou dentro de uma
região distante h/2 do pilar. Para o ACI-
318/2011, a contribuição do concreto
(V
c
) em lajes protendidas pode ser cal-
culada a partir das Equações 2 e 3.
[2]
p
pc
c
p
c
Vdb f
f
V
+
+
=
0
) 3.0 '
(
b
[3]
)
. .
(2 )
. .
(2
y
p
cabos
x
p
cabos
p
sen P n
sen P n V
a
a +
=
Onde:
f
pc
é a tensão de compressão no con-
creto, dado pelo valor média para as
duas direções;
V
p
é a componente vertical de todas as
forças efetivas de protensão que pas-
sam pela seção crítica;
b
p
é o menor valor entre 0,29 ou
(
a
s
d/b
0
+1,5)/12;
b
0
é o perímetro de controle;
d é altura útil.
Para a verificação de elementos es-
truturais protendidos, a NBR6118/2014
utiliza as Equações 4 e 5.
[4]
pd
sd
ef sd
t t
t
- =
,
[5]
du
sen P
i
i
k
pd
.
.
inf,
å
=
a
t
Onde:
t
pd
é a tensão devida ao efeito dos ca-
bos de protensão inclinados que atra-
vessam o contorno considerado e pas-
sam a menos de d/2 da face do pilar;
P
kinf,i
é a força de protensão no cabo i;
a
i
é a inclinação do cabo i em relação ao
plano da laje no contorno considerado;
u é o perímetro crítico considerado;
d é altura útil.
3. ESTUDO DE CASO
O estudo de caso a ser apresenta-
do refere-se à laje de subsolo de uma
edificação comercial projetada pelos
autores. A edificação é constituída de 8
lajes nervuradas protendidas com áre-
as em planta oscilando entre 989 m
2
e
u
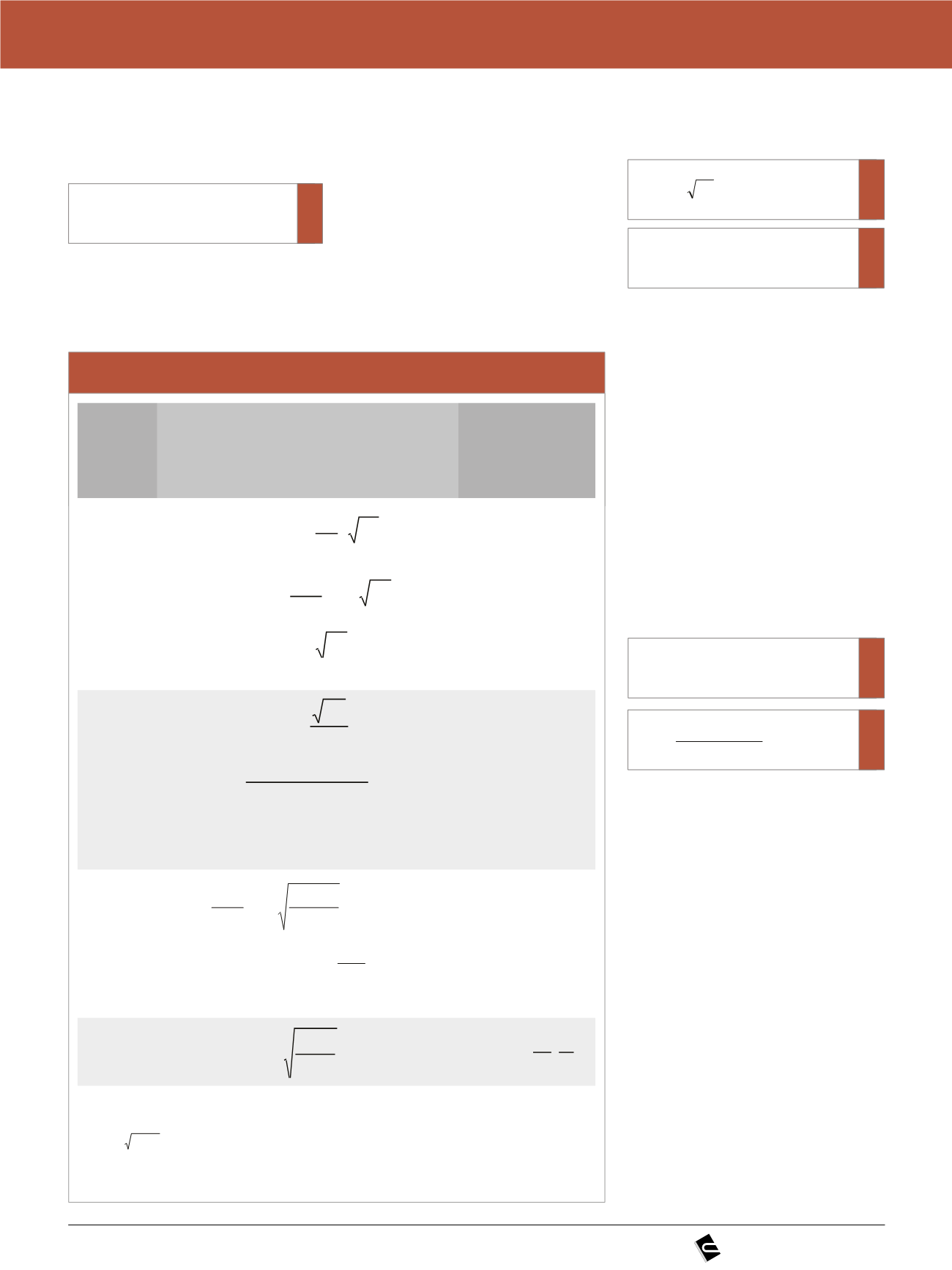
Tabela 2 – Equações utilizadas no cálculo da carga de ruptura de lajes lisas
Normas
Lajes sem
armadura de
cisalhamento
Verificação do
esmagamento
da diagonal
comprimida
do concreto
ACI 318-11
dbf
V
c
c
c
0
'
2
117,0
÷÷
ø
ö
çç
è
æ
+
=
b
dbf
b
d
V
c
s
c
0
'
0
2
083 ,0
÷÷
ø
ö
çç
è
æ
+
=
a
dbf
V
c
c
0
'
33,0
=
Menor valor entre as três equações.
Não há recomendação
fib MC 2010
6,0
. . .6,05,1
1
£
+
=
dg
kd
k
y
y
f
0
ck
Rd
=
c
db
k V
g
y
b
o
– perímetro de controle;
y
– rotação da laje, fora da
região da fissura crítica
da punção.
Não há recomendação
EC2:2004
ud f
f
c
c
÷
ø
ö
ç
è
æ -
=
250
1 3,0 V
Ed
(
)
÷÷
ø
ö
çç
è
æ
+
=
ud f
100ρ
d(mm)
200
1
γ
0,18
V
1/3
ck 1
c
Ed
Menor valor entre as duas equações.
Não há recomendação
ABNT NBR
6118:2014
(
)
dC'
f 100
d(cm)
20
1 0,13
F
1/3
ck
Sd
r ÷
÷
ø
ö
ç
ç
è
æ
+
=
Cd
γ
f
250
f
1 0,27
F
c
ck
ck
Sd
÷
ø
ö
ç
è
æ
-
=
f
ck
, f’
c
: resistência característica à compressão do concreto (MPa);
b
c
: razão entre o comprimento do maior lado sobre o menor lado do pilar;
a
s
: constante que assume os seguintes valores: 40 para pilares internos, 30 para pilares de borda e 20 para pilares de canto;
y x
1
.
rr r r = =
, taxa de armadura nas duas direções ortogonais, obtida utilizando uma largura igual a dimensão do pilar
mais “3d” para cada um dos lados (ou até a borda da laje, se esta estiver mais próxima);
b
0
, u
1
, C e C’: perímetro de controle considerado;
d: altura útil.


