48 | CONCRETO & Construções
u
estruturas em detalhes
Situações limite para
vigas pré-fabricadas
GABRIEL DA MOTTA TREVIZOLI (1) – M
estrando
ROBERTO CHUST CARVALHO – P
rofessor
doutor
ANDREW JOHN RICHTER CASS – M
estrando
LEONARDO MARTINS E SILVA – M
estrando
U
niversidade
F
ederal
de
S
ão
C
arlos
1. INTRODUÇÃO
S
abe-se que a metodologia de cálculo de vigas pré-
-fabricadas protendidas implica uma série de verifi-
cações e considerações normativas que exigem do
engenheiro de projetos uma minuciosa atenção para que não
ocorram erros importantes no dimensionamento dessas peças.
Nelas, a situação de serviço para protensão limitada e completa
pode, muitas vezes, não ter suas condições atendidas.
Além disso, a necessidade de se verificar a intensidade das
tensões em dois tempos distintos (antes e após as perdas de
protensão) pode implicar duas situações conflitantes: no tempo
zero, a protensão é máxima e o carregamento mínimo, e no
tempo infinito, a protensão é mínima e o carregamento máximo.
Situações essas que podem vir a ser mutuamente exclusivas.
Desta forma, propõe-se realizar o dimensionamento de pe-
ças protendidas partindo-se dos limites da área de armadura
ativa (A
p
) para cada verificação em serviço e em vazio. Partindo
das equações de tensão para as verificações em vazio e em
serviço, isola-se a incógnita área da cordoalha e, para cada
situação, verificam-se quais os limites de armadura, que é so-
lução para a inequação. Somando os intervalos de cada verifi-
cação, obtém-se um intervalo comum, que é solução da viga.
Este artigo está inserido na dissertação de mestrado do
autor (Trevizoli – “Programa livre para análise da armadura
longitudinal e da transversal de vigas pré-tracionadas para
diferentes seções”).
2. CONSIDERAÇÕES TEÓRICAS
Partindo do princípio das equações de tensão, isolou-se a
variável armadura de protensão (A
p
) e obteve-se, dessa forma,
um intervalo de resultados que satisfizesse as condições es-
truturais da viga. Fazendo isso para cada uma das condições
normativas, obtém-se um intervalo que seja solução para as
verificações no ELS para o tempo infinito e no ELU em vazio.
As equações de tensão são as seguintes:
[1]
,
*
* *
*
p
p
p
p p
g
q
i
c
i
i
i t
A
A e M M
A
W W W
s
s
s
=¥
Y
=
+
- -
[2]
,
*
* *
*
p
p
p
p p
g
q
s
c
s
s
s t
A
A e M M
A
W W W
s
s
s
=¥
Y
=
-
+ +
Colocadas de forma genérica, onde
σ
i
e
σ
s
são as tensões
na borda inferior e superior, respectivamente.
A NBR 6118:2014 determina os valores limites de tensão
(Tabela 1).
Abaixo são apresentadas as inequações de equilíbrio utili-
zadas para definição dos intervalos, derivadas das equações
de tensão, seguido de uma breve explicação.
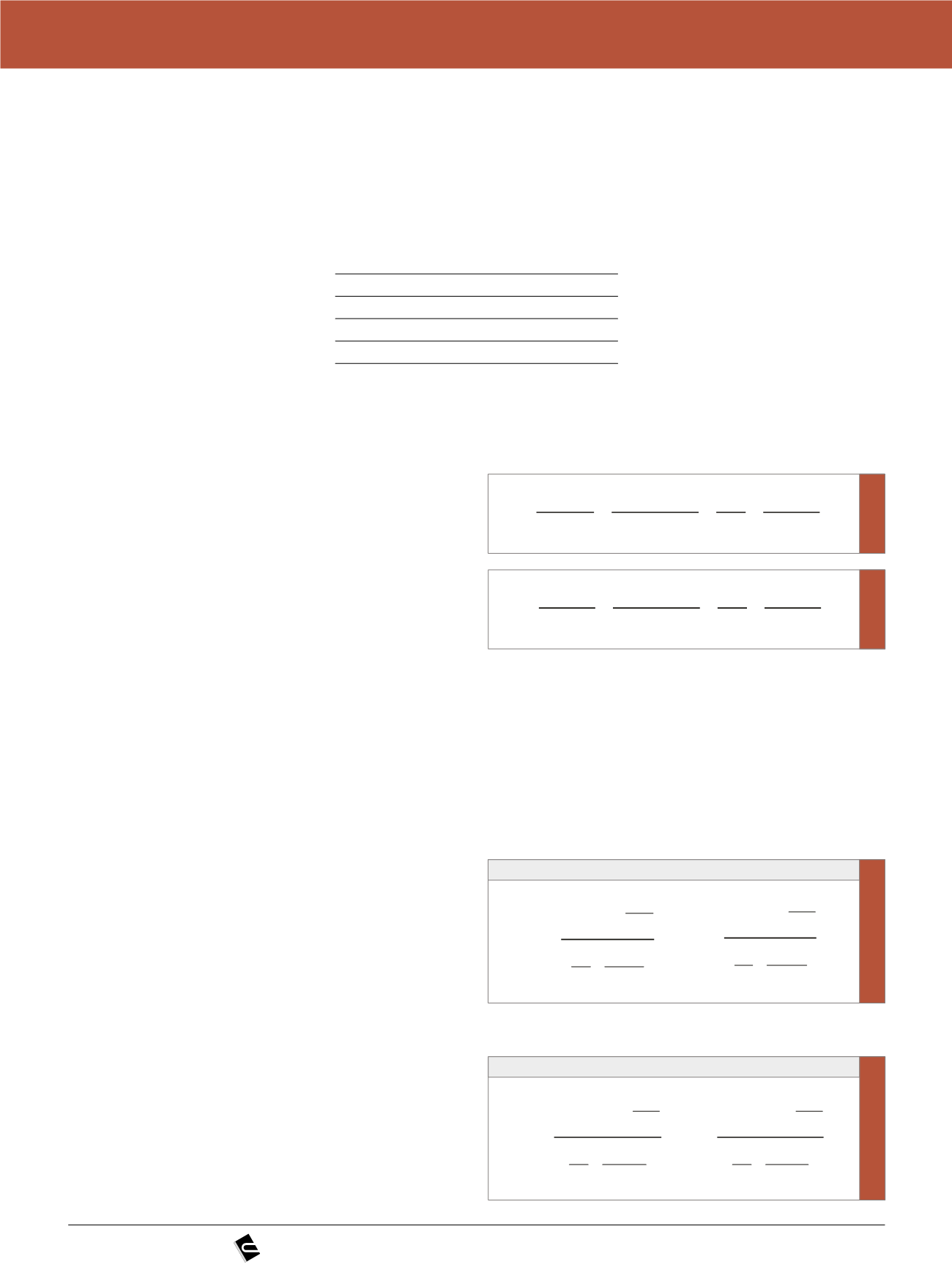
a-) Verificação de compressão excessiva no tempo zero:
[3]
Borda inferior
Borda superior
1
,
0,7*
*
g
ckj
i
p
p
p p
c
i
M
f
W
A
e
A W
s s
+
£
+
1
,
0,7*
*
g
ckj
s
p
p
p p
c
s
M
f
W
A
e
A W
s s
-
£
-
b-) Verificação de limite de tração no tempo zero:
[4]
Borda inferior
Borda superior
1
,
1,2*
*
g
ctm
i
p
p
p p
c
i
M
f
W
A
e
A W
s s
-
+
³
+
1
,
1,2*
*
g
ctm
s
p
p
p p
c
s
M
f
W
A
e
A W
s s
-
-
³
-


