CONCRETO & Construções | 33
[2]
(
)
Σ
Σ
2 3 140 1,487 200 0,435 2 711,54
p s
p pyd
s yd
R A f
A f
kN
+
=
+
= ´ ´ ´ + ´
= ´
Donde a altura do bloco de tensões no banzo comprimido,
com
c
p s
R R
+
=
:
[3]
2 711,54/(0,0243 2400) 24,4
0,85
c
cd fl
R y
mm
f b
=
= ´
´ =
Com este valor, obtêm-se os braços de alavanca das arma-
duras ativa e passiva:
[4]
E o momento resistente:
[5]
(
Σ
Σ
2 624, 54
d
p pyd p
s yd s
M A f z
A f z
=
+
= ´
´
)
0, 4478 87 0, 5398 677, 7
kNm
+ ´
=
pouco maior que o momento solicitante no centro do vão:
[6]
(
)
2
2
1
12
1, 4 26, 82
675, 9
8
8
Sd
f
o
l
M g g q
kNm
g=
+ + = ´ ´ =
O braço de alavanca resultante da armadura mista é:
[7]
(
)
677,7/ 2 711,54 0,476
d
p s
M
z
m
R
+
= =
´
=
2.3 ELU-Força cortante
2.3.1 M
ontagem
da
treliça
resistente
da nervura
Aplica-se o modelo de treliça resultante de campos de ten-
são, tanto nas nervuras do
π
quanto nos flanges. As treliças
são examinadas a seguir. A escolha da inclinação das diago-
nais comprimidas, cf. o MC2010, atualmente é mais restrita e
se dá na faixa
45
min
θ
θ
°
≤ ≤
, em que
25
min
θ
°
=
nas peças com
força normal de compressão significativa ou protendida. An-
teriormente, no MC90, tinha-se
18, 43
min
θ
°
=
. Vale mencionar os
demais limites:
30
min
θ
°
=
nas peças de concreto armado (caso
do flange do exemplo) e
40
min
θ
°
=
nas peças com força nor-
mal de tração significativa (caso de talão, se houvesse). No
exemplo, escolhe-se
25, 45
θ
°
=
, e com
0, 476
z
m
=
, resultam
seis segmentos de comprimento
0, 476 25, 45 1
zcot
cot
m
θ
°
=
=
,
em cujos pontos médios são posicionadas as seis cargas
nodais equivalentes da treliça (i.e., na treliça e na viga têm-
-se iguais reações de apoio e momentos fletores sob as
cargas nodais):
u
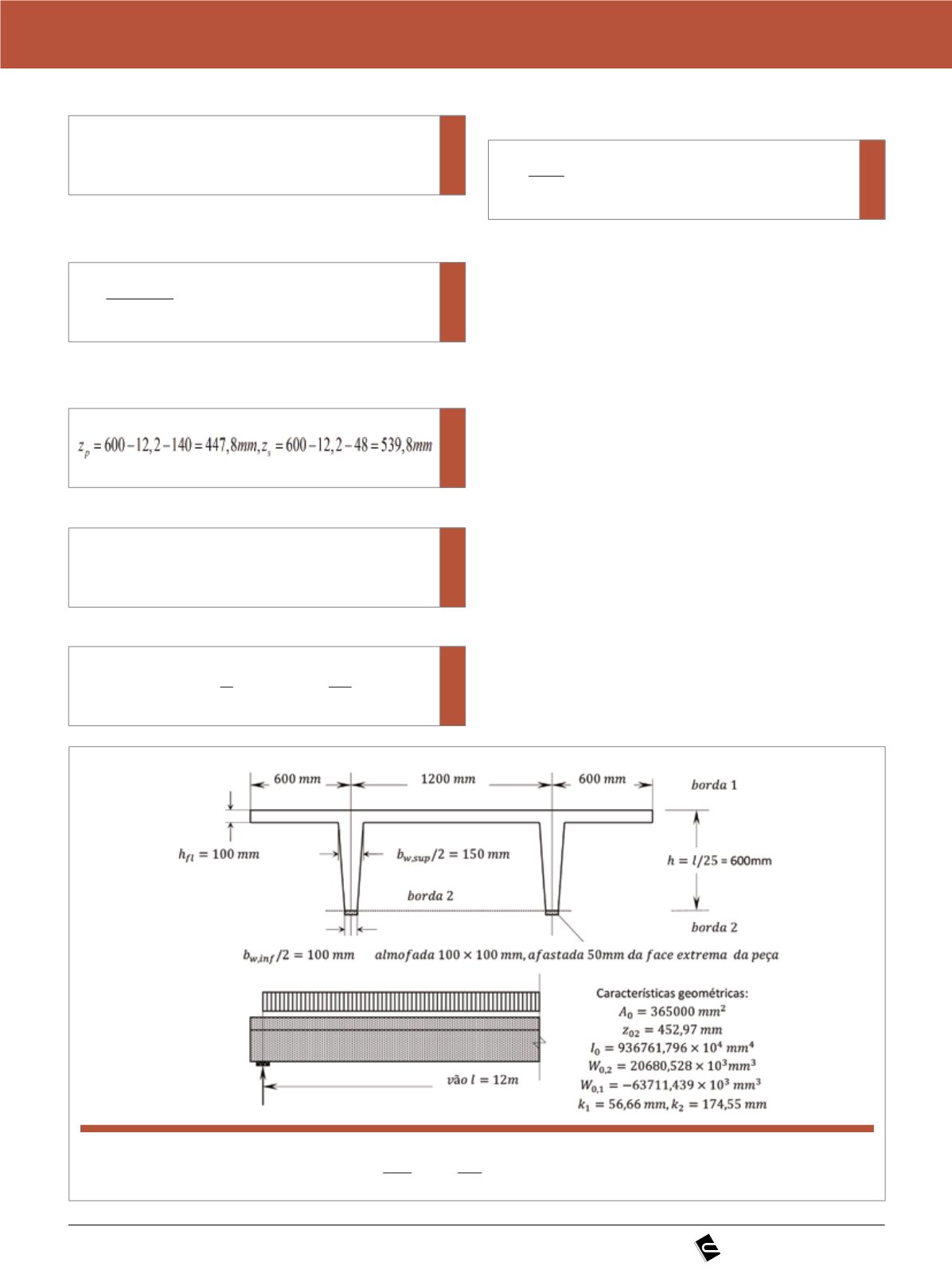
Figura 1
Viga para piso com carga variável de
p
2
500
kg f
m
(
2
5 )
kN
ou
m


