80 | CONCRETO & Construções
também pretende-se garantir a ductili-
dade da seção restringindo-se a altura
da linha neutra, porém consideram-se
os valores limite para a profundidade
relativa da linha neutra dados pela edi-
ção de 2014 da ABNT NBR:6118 [3],
mostrados na Equação 37.
[37]
Então, se o valor de k
x
encontrado
respeitar esses valores, tem-se uma
peça no domínio 3 com boa ductili-
dade, mas se o valor for maior, tem-
-se uma peça com pouca ductilidade,
mesmo ainda estando no domínio 3,
devendo-se alterar as dimensões da
seção e utilizar um concreto com maior
resistência à compressão ou calculá-la
com armadura dupla.
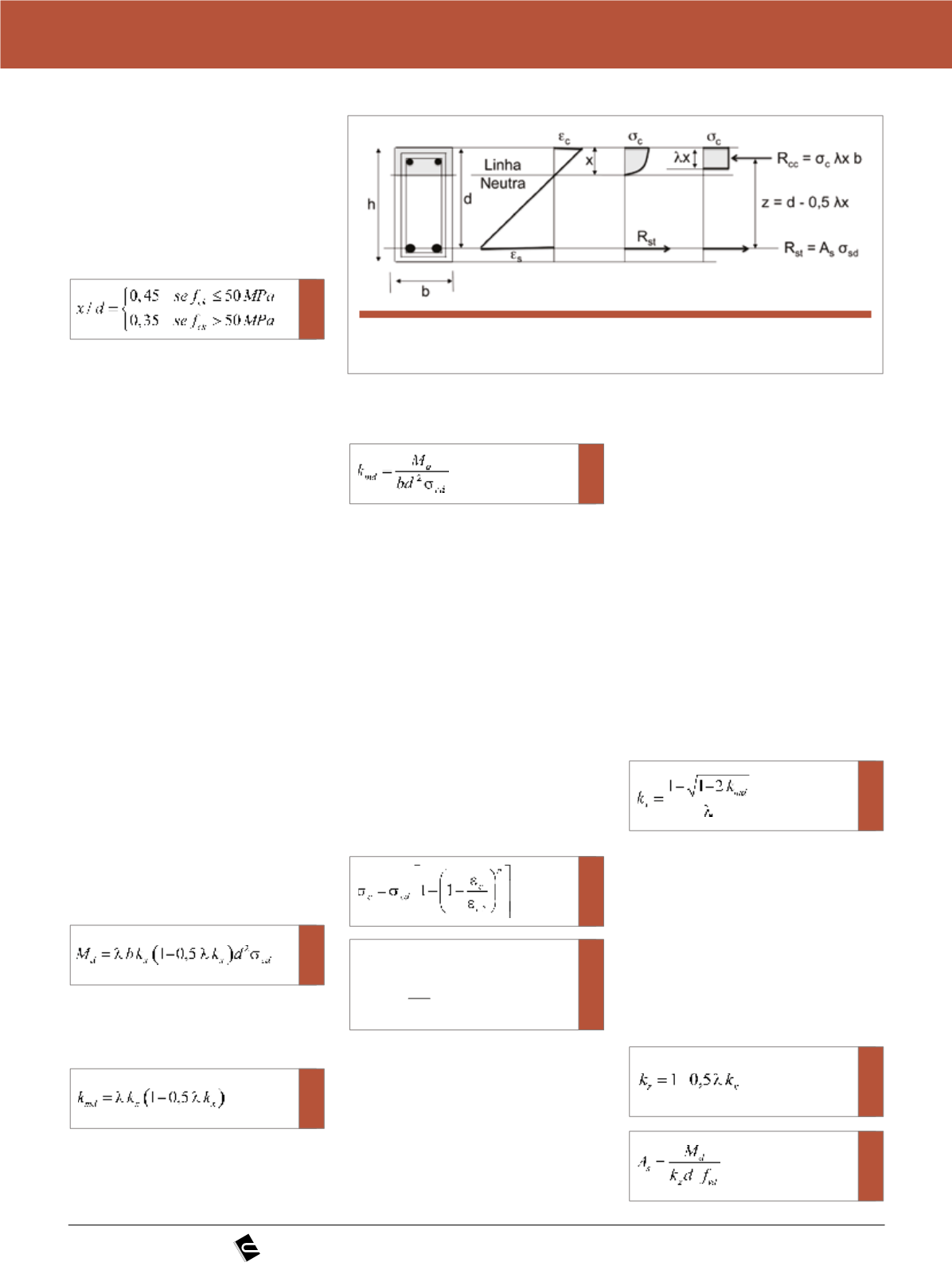
Considerando as prescrições da
norma brasileira [3], pode-se fazer o
dimensionamento no ELU utilizando
o diagrama retangular simplificado de
tensões, como mostrado na Figura 7.
Aqui serão considerados os valores
de
a
c
e
λ
dados pelas equações 17
e 18.
Fazendo então o equilíbrio de mo-
mentos da seção, considerando as
resultantes apresentadas na Figura 7 e
que
s
c
=
s
cd
=
a
c
f
cd
, chega-se, em pro-
cedimento semelhante ao de Araújo [5],
à expressão:
[38]
Com isso, pode-se redefinir o coefi-
ciente k
md
apresentado por Clímaco [4],
como:
[39]
Substituindo na Equação 38 pode-
-se expressar o valor do k
md
em função
do momento fletor solicitante, da geo-
metria da seção e das características
do concreto utilizado:
[40]
Essa equação considera a tensão
última do concreto, ou seja, que o con-
creto foi esmagado, porém, no domínio
2, como já foi dito anteriormente, não
se pode considerar o esmagamento do
concreto. Assim, deve-se utilizar um valor
para a tensão mais próximo da realida-
de. Essa tensão é encontrada através da
Equação 39, adaptada da equação dada
pela norma [3] para a tensão no trecho
parabólico do diagrama parábola-retân-
gulo, sendo o valor de n conforme as ex-
pressões 40 e o valor de
e
c
=
e
cd
obtido
da Equação 2, fazendo
e
sd
= 10‰.
[41]
[42]
4
ck
ck
2,0
n=
90-f
1,4+23,4
para
concretos com 50<f
90 MPa
100
ì
ï
í
æ
ö
ï
ç
÷
è
ø
î
ck
para concretos com f
50 MPa
£
£
A norma brasileira [3] considera,
para o cálculo da tensão
s
c
, o valor
0,85 f
cd
ao invés de
s
cd
, que é usado na
Equação 41. Porém, como as fórmulas
usadas no modelo generalizado são
deduzidas a partir do diagrama simpli-
ficado de tensões, não se pode consi-
derar uma tensão maior que a tensão
máxima
s
cd
=
a
c
f
cd
. Isso é necessário,
pois, para concretos das classes C55 a
C90, o valor de
a
c
é menor que 0,85, o
que resultaria, para deformações pró-
ximas ao valor de
e
c2
, em valores da
tensão corrigida maiores que o valor
da tensão máxima
s
cd
, caracterizando-
-se em uma inconsistência, já que, no
domínio 2, a tensão no concreto não
atinge o valor máximo.
A partir da Equação 39 encontra-se
uma expressão para a profundidade re-
lativa da linha neutra em função do coe-
ficiente adimensional do momento fletor:
[43]
Sendo o coeficiente do braço de
alavanca k
z
dado pela Equação 42, a
partir do equilíbrio de momentos para
o aço a tração e, desenvolvendo uma
equçação semelhante à Equação 14,
pode-se calcular o valor da área de aço
necessária ao equilíbrio da seção a par-
tir da Equação 45.
[44]
[45]
u
Figura 7
Seção de viga no ELU (FONTE: autor, 2015)


