76 | CONCRETO & Construções
domínios de deformação, de forma a
simplificar o cálculo e facilitar o seu en-
sino e aprendizagem, permitindo uma
visualização e entendimento melhores
de como se dá o dimensionamento de
elementos submetidos à flexão.
2. DIMENSIONAMENTO À FLEXÃO
SEGUNDO ALGUNS AUTORES
Segundo Clímaco [4], dimensionar
uma peça à flexão consiste, basicamen-
te, de duas etapas: a primeira é encon-
trar as dimensões da seção transversal
da peça e a área das armaduras, obti-
das para um momento fletor de cálcu-
lo (M
Sd
); e a segunda é a verificação do
comportamento da peça aos Estados
Limites de Serviço (ELS). Para o dimen-
sionamento da armadura de flexão ele
diz que as expressões devem ser obti-
das por duas vias: a compatibilidade de
deformações, baseada na hipótese das
seções planas de Bernoulli, e o equilíbrio
da seção, imposto pela condição de que
o momento M
Sd
deve ser menor ou igual
ao binário composto pelas resultantes
de compressão no concreto (R
cc
) e de
tração no aço (R
st
), que compõem o mo-
mento resistente M
Rd
= R
cc
. z = R
st
. z,
conforme mostrado na Figura 1.
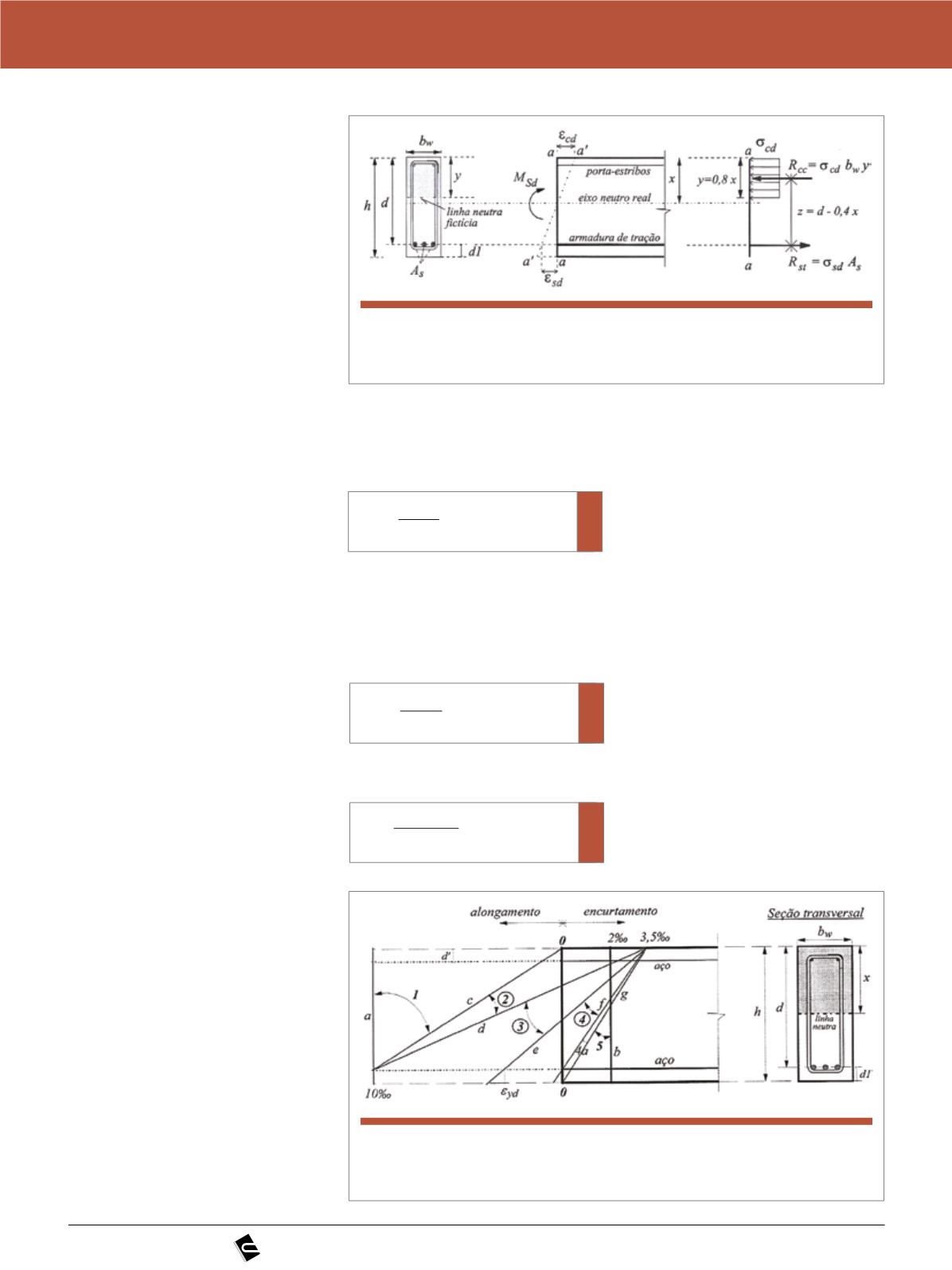
À esquerda da Figura 1, são apre-
sentados os detalhes de uma seção
transversal retangular com armadura
simples. No centro, é representado
um corte longitudinal onde são mos-
tradas as deformações específicas de
encurtamento do concreto (
e
cd
) e de
alongamento do aço (
e
sd
). À direita, é
mostrado o diagrama retangular sim-
plificado dado pela edição de 2007 da
ABNT NBR:6118 [1], onde
s
cd
= 0,85
f
cd
é a tensão última de compressão no
concreto, x é a profundidade da linha
neutra da seção e
s
sd
é a tensão de tra-
ção máxima na armadura. Consideran-
do a compatibilidade de deformações
do aço e do concreto e, analisando a
rotação da seção, por semelhança de
triângulos obtêm-se:
[1]
cd
sd
x
d x
e
e
=
-
Clímaco [4] propõe o coeficiente
adimensional k
x
= x/d, que representa
a profundidade relativa da linha neu-
tra. Assim, a deformação específica
e
cd
pode ser expressa como:
[2]
1
x
cd
sd
x
k
k
e
e
=
-
E o coeficiente k
x
pode ser encon-
trado com a Equação 3.
[3]
cd
x
cd
sd
k
e
e e
=
+
A partir dessa equação e, conside-
rando os domínios de deformação das
seções no Estado Limite Último (ELU),
ilustrados na Figura 2, Clímaco [4] apre-
senta os seguintes intervalos para os
valores do coeficiente k
x
, definidos pe-
los limites das deformações máximas
do concreto e do aço:
u
Limite entre os domínios 1-2:
k
x
= 0
u
Limite entre os domínios 2-3:
k
x
= 0,259
u
Limite entre os domínios 3-4:
k
x
= 3,5‰ / (3,5‰ +
e
yd
)
u
Limite entre os domínios 4-4a:
k
x
= 1
Com isso, percebe-se que, varian-
do o coeficiente k
x
no intervalo de 0 a
1, pode-se definir todas as situações
u
Figura 1
Seção retangular com armadura simples no estado limite último
(FONTE: Clímaco, 2013)
u
Figura 2
Domínios de deformação das seções no estado limite último
(FONTE: Clímaco, 2013)


