CONCRETO & Construções | 79
Assim, a Equação 25 fica:
[26]
Dessa equação pode-se definir o
parâmetro adimensional µ:
[27]
Então a Equação 26 fica:
[28]
Araújo [5] define o momento limite re-
duzido
m
lim
, dado na Equação 29, onde
x
lim
é o valor limite para x/d, dado na Equação
19, que depende do concreto utilizado.
[29]
E da Equação 28 tem-se a expressão
do momento solicitante reduzido µ, em
função do momento fletor solicitante M
d
:
[30]
Assim, para o dimensionamento à
flexão simples deve-se calcular o parâ-
metro µ e compará-lo com o valor limi-
te
m
lim
. Se µ
≤
m
lim
, o dimensionamento
deve ser feito com armadura simples.
Mas se µ >
m
lim
, deve-se dimensionar a
seção com armadura dupla. Para essa
última condição, não significa que a viga
esteja no domínio 4, apenas pretende-
-se garantir a ductilidade da seção an-
tes que esse domínio seja atingido.
Resolvendo a Equação 27 em fun-
ção do adimensional
ξ
, encontram-se
duas raízes, porém apenas uma delas
indica que a linha neutra cai dentro da
seção transversal, sendo a única que
tem o significado correto. A solução é
dada pela Equação 31.
[31]
Fazendo, agora, o equilíbrio de for-
ças para as resultantes dadas na Figura
5, tem-se:
[32]
[33]
Fazendo x =
ξ
d, com
ξ
obtido da
Equação 31, e substituindo na Equação 33:
[34]
Assim, o dimensionamento à flexão
com armadura simples, de acordo com
Araújo [5], se reduz a encontrar os valo-
res de µ,
ξ
e A
s
, utilizando as equações
30, 31 e 34, respectivamente. Porém,
esse método não considera a variação
da tensão atuante no concreto quando
a peça estiver no domínio 2, uma sim-
plificação que pode resultar em uma
área de aço menor que a necessária.
3. APRESENTAÇÃO DO MODELO
GENERALIZADO
O modelo de dimensionamento pro-
posto também considera o coeficiente
adimensional k
x
dado na Equação 3,
porém aqui utiliza-se o diagrama de do-
mínios de deformação no Estado Limite
Último (ELU) dado pela norma [3] e re-
presentado na Figura 6, a partir da qual,
por semelhança de triângulos, pode-se
definir os limites entre os domínios atra-
vés dos valores de k
x
, como mostrado
a seguir:
u
Limite entre os domínios 1-2:
k
x
= 0
u
Limite entre os domínios 2-3:
k
x
=
e
cu
/(
e
cu
+ 10‰)
u
Limite entre os domínios 3-4:
k
x
=
e
cu
/(
e
cu
+
e
yd
)
u
Limite entre os domínios 4-4a:
k
x
= 1
Na Figura 6, os valores de
e
cu
e
e
c2
são dados por:
[35]
cu
3,5 ‰
ε =
ì
ï
í
ï
î
4
ck
ck
90-f
2,6 ‰+35 ‰
para
concretos com 50<f 90 MPa
100
æ
ö
ç
÷
è
ø
ck
para concretos com
f
50 MPa
£
£
[36]
c2
2,0 ‰
ε =
ìï
í
ïî
(
)
ck
0,53
ck
ck
para concretos com f
50 MPa
2,0 ‰+0,085 ‰ f -50 para concretos com 50<f
90 MPa
£
£
Assim como Araújo [5], aqui
u
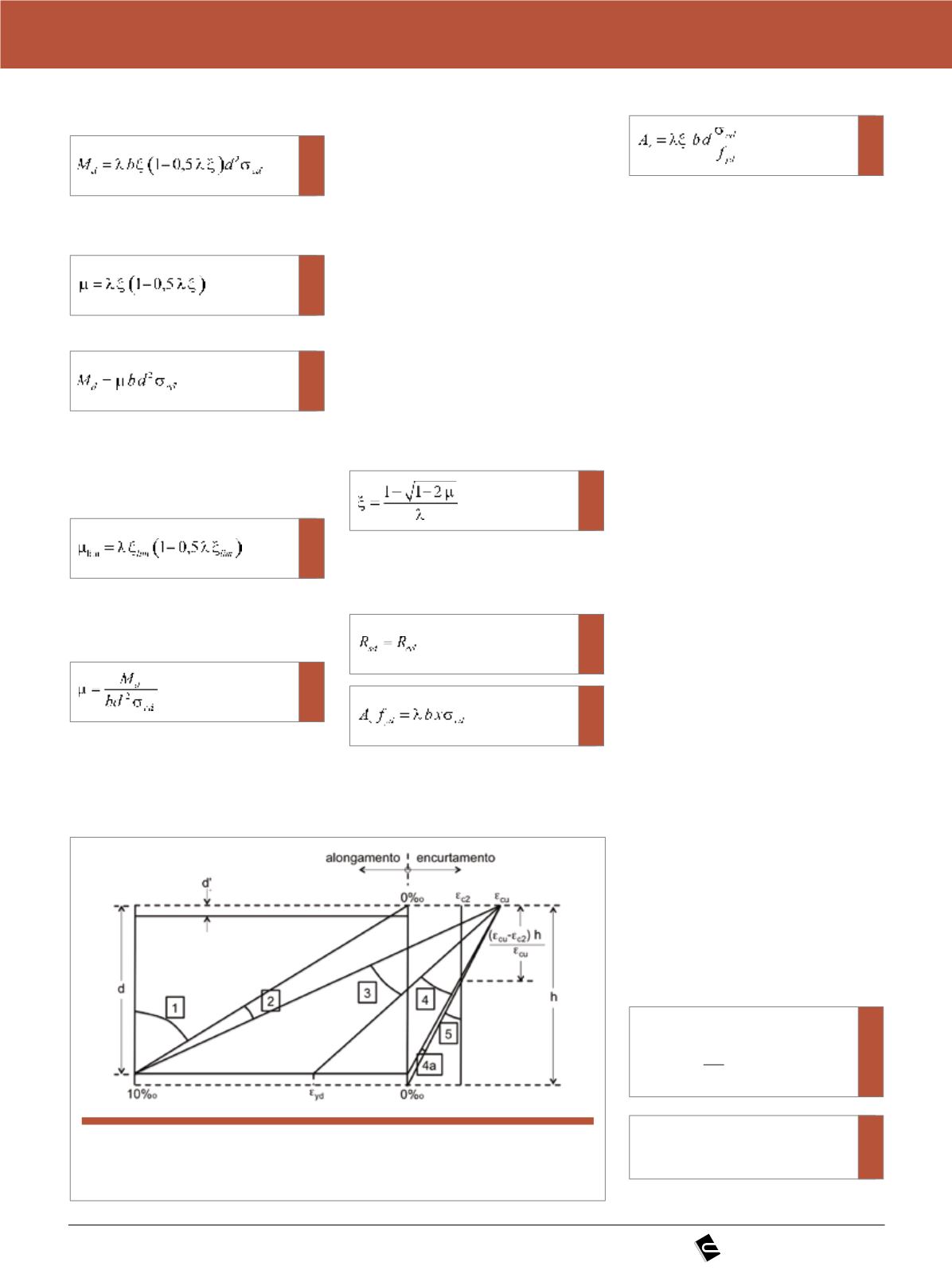
Figura 6
Domínios de deformação no ELU de uma seção transversal
(FONTE: ABNT NBR 6118, 2014)


