CONCRETO & Construções | 77
possíveis do dimensionamento de se-
ções de concreto submetidas à flexão
simples.
Analisando novamente a Figura 1 e,
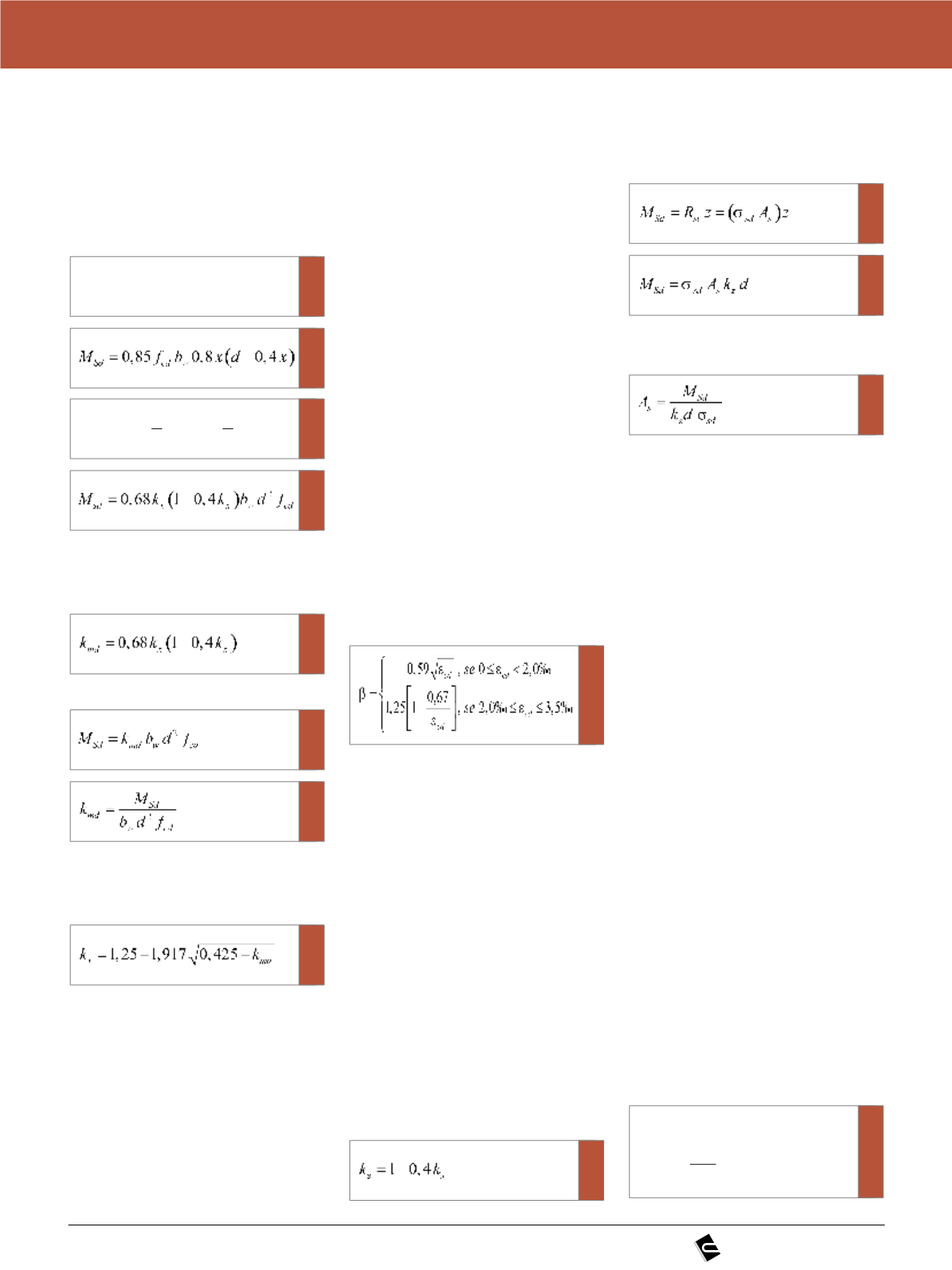
fazendo o equilíbrio de momentos para
o concreto à compressão, tem-se:
[4]
(
)(
)
0, 4
Sd
cc
cd w
M R z
b y d x
s
= =
-
[5]
[6]
2
0,68
1 0, 4
Sd
w cd
x
x
M
b d f
d
d
é
ù
æ ö
æ ö
=
- ç ÷
ç ÷
ê
ú
è ø
è ø
ë
û
[7]
Da Equação 7, pode-se obter o co-
eficiente do momento de cálculo k
md
através da seguinte definição:
[8]
Substituindo na Equação 7:
[9]
[10]
Resolvendo a Equação 8, de grau 2
em k
x
, obtém-se uma expressão para
k
x
em função de k
md
:
[11]
Com isso, conhecendo as dimen-
sões da seção transversal, a resistência
à compressão do concreto e o momen-
to solicitante, encontra-se o valor de k
md
a partir da Equação 10. Substituindo
esse valor na Equação 11 obtém-se o
valor de k
x
e o correspondente domínio
em que a peça se encontra. Porém, a
Equação 10 foi deduzida para a tensão
última de compressão no concreto
s
cd
= 0,85 f
cd
. Para essa tensão su-
põe-se que o concreto seja esmaga-
do, o que não ocorre em peças no
domínio 2, ou seja, para valores de
k
x
menores que 0,259, é necessário
considerar a tensão real atuante no
concreto.
Clímaco [4] apresenta então o
coeficiente
β
de correção dessa
tensão, dado pelas expressões da
Equação 12, considerando as de-
formações do concreto no domínio
2. Esse coeficiente é encontrado
igualando-se as resultantes R
cc
dos
diagramas parábola-retângulo e re-
tangular simplificado, dados pela
ABNT NBR:6118 [1], e analisando a
compatibilidade de deformações na
zona comprimida de concreto a par-
tir de princípios básicos da Mecânica
dos Sólidos.
[12]
Nas expressões da Equação 12,
a deformação
e
cd
é dada em ‰ e
calculada com a Equação 2, utilizan-
do o valor de k
x
encontrado com a
Equação 11. Com isso, calcula-se
um novo coeficiente do momento,
k
md,cor
, dividindo o valor obtido com a
Equação 10 pelo valor de
β
e subs-
titui-o na Equação 11, encontrando
uma nova profundidade relativa da
linha neutra, k
x,cor
, agora consideran-
do uma tensão de compressão mais
próxima da real.
Da Equação 7 pode-se definir
também o coeficiente do braço de
alavanca k
z
= z/d, em função de k
x
:
[13]
Fazendo agora o equilíbrio de mo-
mentos para o aço a tração, a partir da
Figura 1, tem-se:
[14]
[15]
De onde se obtém a área de aço
necessária ao equilíbrio:
[16]
Assim, calcula-se k
z
com o valor de
k
x
, ou k
x,cor
, e então encontra-se a área
de aço da armadura com a Equação
16, onde
s
sd
é igual à tensão de escoa-
mento do aço f
yd
.
Esse roteiro de dimensionamento
foi desenvolvido considerando o dia-
grama retangular simplificado proposto
pela ABNT NBR:6118 [1], que conside-
ra apenas concretos com resistência à
compressão inferior ou igual a 50 MPa.
Assim, o dimensionamento para concre-
tos do grupo II de resistências não pode
ser feito utilizando essas expressões.
Araújo [5] propõe um modelo de
dimensionamento baseado na edição
de 2014 da ABNT NBR:6118 [3], que
também abrange concretos das clas-
ses C55 a C90. Para isso, ele utiliza o
diagrama retangular de tensões dado
em [3] e representado na Figura 3.
Conforme mostrado nessa figura,
admite-se que a tensão no concreto seja
dada por
s
cd
=
a
c
f
cd
, desde a borda mais
comprimida da seção até uma distância
l
x, onde x é a profundidade da linha neu-
tra. Os valores de
a
c
e
λ
são dados por:
[17]
c
ck
ck
0,85
f 50
0,85 1
paraconcretoscom 50 f 90MPa
200
ck
para concretos com
f
50 MPa
£
ì
ï a = é
- ù
í
æ
ö
-
< £
ç
÷
ê
ú
ï
è
ø
ë
û
î


