CONCRETO & Construções | 63
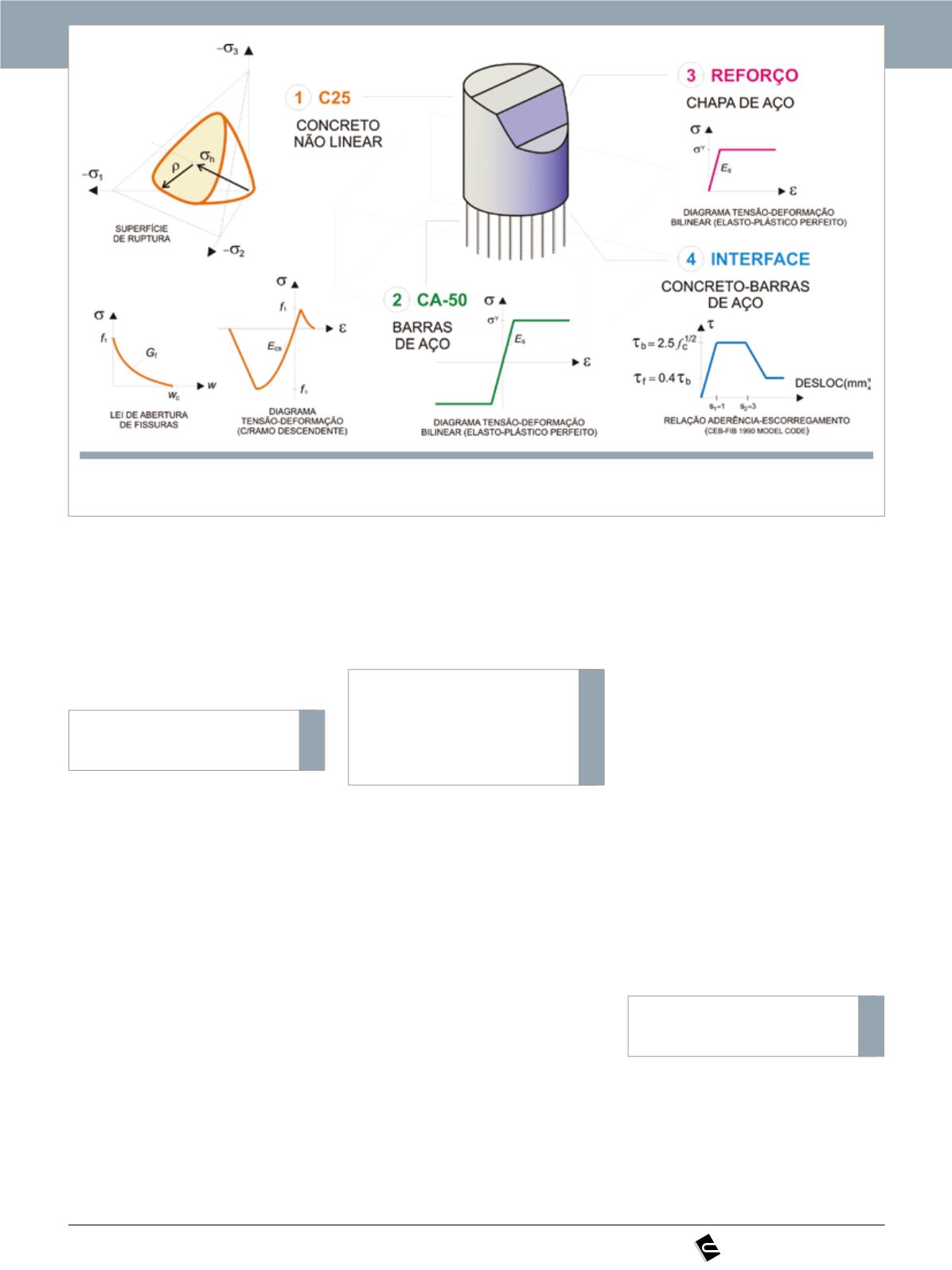
nas suas interfaces é esquematizado
na Figura 2.
A equação constitutiva para o esta-
do triplo de tensões com acoplamento
termo-estrutural de materiais elásticos-
-lineares de comportamento ortotrópi-
co, é definida por:
[1]
T
D× + × =
ασCε
onde
e
={
e
x
,
e
y
,
e
z
,
g
xy
,
g
yz
,
g
zx
},
s
={
s
x
,
s
y
,
s
z
,
t
xy
,
t
yz
,
t
zx
},
a
={
a
x
,
a
y
,
a
z
,
0, 0, 0} são as deformações (lineares e
distorções), as tensões (normais e tan-
genciais) e os coeficientes de expan-
são térmica, respectivamente. As ten-
sões e a matriz de rigidez da estrutura,
dada por D = C
-1
, podem ser decom-
postas nas parcelas s = s
c
+ s
r
+ s
s
e
D = D
c
+ D
r
+ D
s ,
relativas ao concreto,
armaduras e chapas de reforço. Desse
modo, pode-se acessar os níveis de ten-
são e de deformação em cada material.
2.3 Modelo constitutivo para
o concreto afetado pela RAA
A expansão por RAA é significativa-
mente influenciada pelo estado triaxial
de tensões. Segundo o modelo adapta-
do de Charlwood (LÉGER, 1995), a influ-
ência do estado de tensão na expansão
por RAA pode ser representada por:
[2]
( )
L i
U i
L
i
U
i
g
i
10
u g
u g
g
para
para
para
para
0 ε
σ/σ log
ε ε
ε ε
0 ε
U
s s
s s s
s s
s
<
£ £
< £
³
=
× - =
=
=
ï
ï
ï
î
ïï
ï
í
ì
ef
ef
tf
tf
K
Onde:
e
g
é a taxa de expansão por RAA de um
elemento parcialmente confinado (em
me
/ano –“microdeformação/ano”);
e
u
é a taxa de expansão por RAA de um
elemento desconfinado (expansão livre)
s
i
é a tensão principal na direção
analisada;
s
U
é o limite superior de tensão, acima
do qual o efeito do confinamento é inó-
cuo em termos de expansão por RAA;
s
L
é o limite inferior de tensão, abaixo
do qual a expansão por RAA é total-
mente inibida;
f
t
ef
é a resistência à tração efetiva cal-
culada, por exemplo, pelo critério de
Willan-Warnke.
Quando a resistência à tração
for atingida, inicia-se o processo de
microfissuração interrompendo a ex-
pansão por RAA. A Figura 3 apresen-
ta o modelo teórico utilizado neste
trabalho, que considera a dependên-
cia do estado triaxial de tensão com
as expansões ortogonais por RAA,
conforme descrito anteriormente.
De acordo com esta metodologia,
a expansão química por RAA pode
ser considerada análoga à expan-
são térmica, a partir da calibração
dos coeficientes de expansão tér-
mica equivalentes com os dados
experimentais. Considerando-se,
arbitrariamente, a variação da tem-
peratura e o incremento de tempo
unitários, pode-se escrever:
[3]
j
i
j
ig,
ε
a=
Sendo:
i = x,y,z (direção analisada);
j = 1,2,3,…(tempo)
a
i
o coeficiente de expansão tér-
mica linear para comportamento
ortotrópico.
u
Figura 2
Caracterização de parâmetros dos materiais considerados no modelo matemático


