CONCRETO & Construções | 37
u
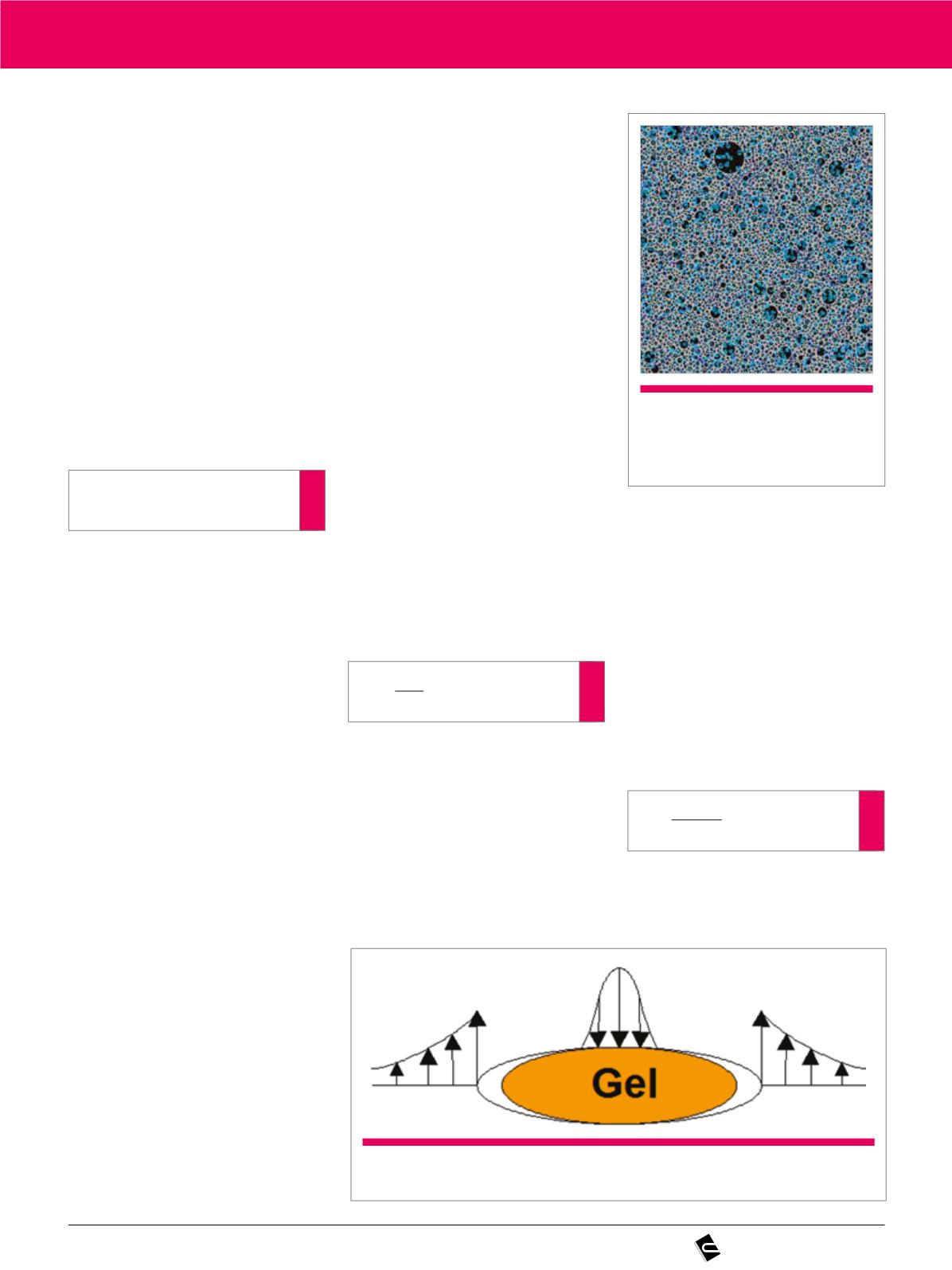
Figura 7
Mapeamento das zonas da
amostra que estão sob tensão
(DUNANT; SCRIVENER, 2010)
de seu acondicionamento, uma vez
que a argamassa está sob compres-
são com o nível de tensões próxi-
mas ao seu estado limite. Pode-se
observar na Figura 7 a malha com
a distribuição das tensões sobre os
agregados, a qual gera compressão
na argamassa.
A expansão do gel é dada confor-
me a Equação 4, em que
Ω
gel
corres-
ponde à superfície do gel, e, ao ele-
mento de superfície, h
i
, à função de
forma associada ao grau de liberda-
de considerado, f
i
, à força associada
e E, ao tensor de tensão do gel.
[4]
(
)
imp
Ω
d Ω
-
= Ñ
Ç
Ç
ò
f
E
gel
e
i
i
gel
e
h
e
3.3.3 M
odelo
preditivo
na
escala
macroscópica
– C
apra
e
S
ellier
(2003)
Segundo Capra e Sellier (2003),
a dificuldade para modelação da re-
ação álcali-agregado se dá devido
à distribuição aleatória dos locais
com reatividade e ao escasso co-
nhecimento da química e dos me-
canismos que envolvem as reações.
Todavia, baseando-se em uma des-
crição probabilística dos principais
parâmetros físicos do concreto e da
RAA, é possível simular a expansão
a que o material está sujeito. Para
tanto, modela-se o concreto como
um material sujeito à fissuração com
tensões elásticas e inelásticas. A
RAA é modelada levando em consi-
deração a temperatura, a umidade,
o estado de tensões e a cinética da
reação. Os autores propõem, ainda,
a verificação da probabilidade de
abertura de fissuras.
Antes de desenvolverem a mo-
delagem para a RAA, os autores
descrevem o comportamento do
concreto baseando-se na descri-
ção da sua deterioração por meio
da criação de uma superfície de
descontinuidade.
A parte elástica do comporta-
mento do concreto baseia-se na te-
oria ortotrópica de danos, proposta
por Lemaitre e Chaboche (1988
apud
CAPRA; SELLIER, 2003). O estado
do material, em termos de rigidez, é
dependente de uma variável fenome-
nológica “d”, a qual é definida como
a razão entre a superfície de des-
continuidade (fissuras, vazios, etc) e
a superfície total da amostra, sendo
que seu valor varia entre 0 e 1.
De posse do valor do coeficien-
te “d” é possível calcular a tensão
efetiva através da Equação 5, sendo
esta dada pela relação entre a ten-
são aparente
σ
app
e o coeficiente de
dano “d”.
[5]
1
=
-
app
eff
d
s
s
As deformações e as tensões
aparentes são calculadas conforme
as tensões efetivas, baseando-se no
trabalho de Sellier
et al.
(2001
apud
CAPRA; SELLIER, 2003).
Partindo-se para a modelação da
reação, verificam-se as tensões de
equilíbrio geradas pela RAS, isto é,
sem uma carga externa, a amostra
de concreto sujeita à reação, que
expande, surgindo uma tensão de
autoequilíbrio dentro do material (Fi-
gura 8).
Sendo P
g
a pressão média exer-
cida pelos produtos da matriz ci-
mentícia e
σ
gi
a tensão induzida pelo
material sem dano. A equação de
equilíbrio leva à relação expressa
pela Equação 6, válida para as três
direções principais “i”.
[6]
1
=
-
g
gi
aari
P
Pf
s
em que: Pf
aari
representa a probabi-
lidade de fissuração na direção “i” e
(1 - Pf
aari
) é a fração de material não
u
Figura 8
Tensões de equilíbrio geradas pela RAA (CAPRA; SELLIER, 2003)
s
gi
s
gi
P
g


