36 | CONCRETO & Construções
u
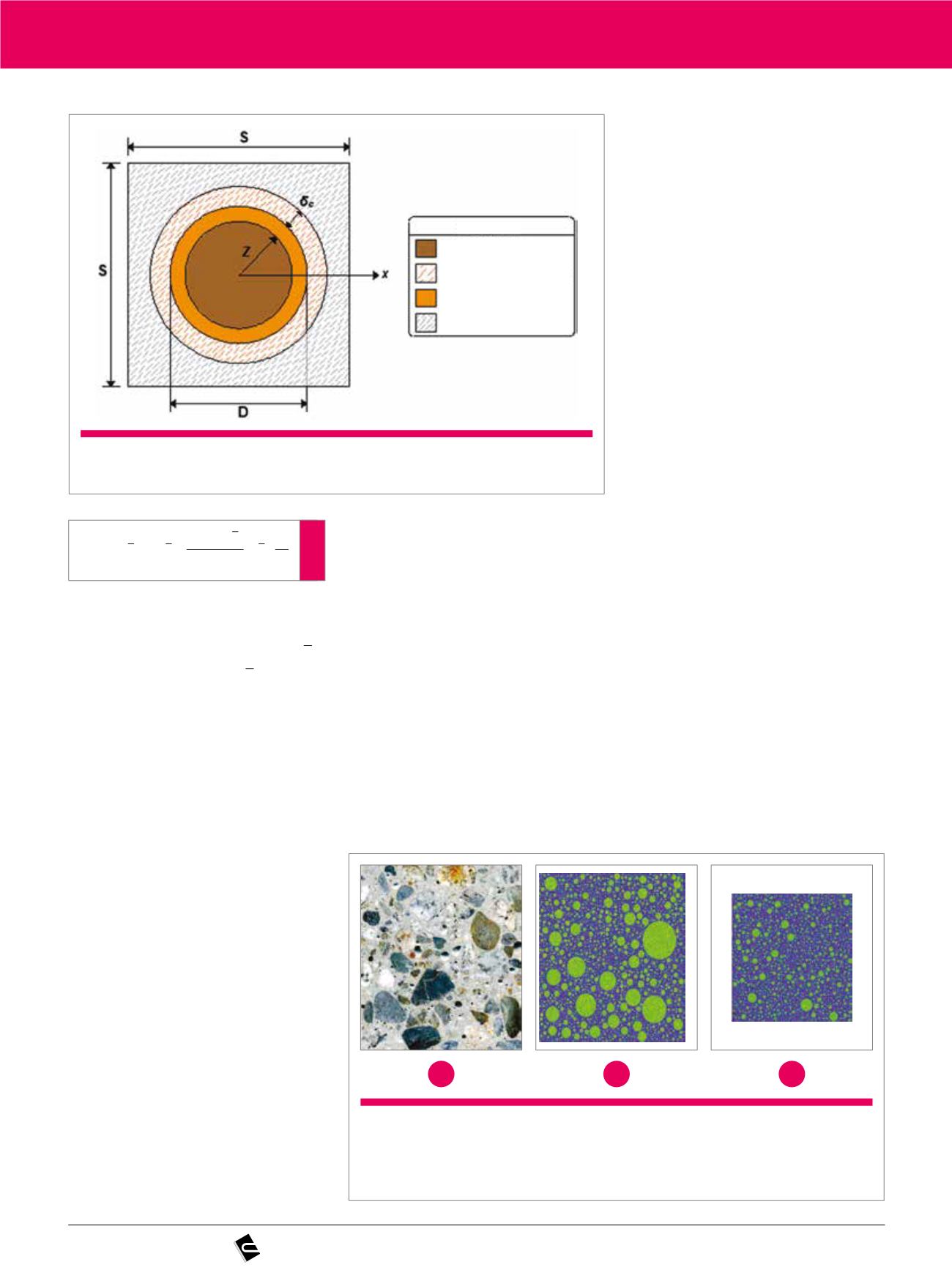
Figura 5
Modelo de célula cúbica idealizada por Bazant e Steffens
Legenda
Partícula sem reagir
Região de acomodação do gel
Partícula com reação
Célula cúbica
[3]
( ) ( ) (
)
(
)
1 2 /
2
,
,
2 /
-
=
=
=
w s
z Dx
x
w F x F x
x
z D
D
x
em que:
ξ
w
corresponde à concentra-
ção de sílica, w
s
, à concentração de
água nos poros da partícula, F
( )
x
,
ao perfil dimensional e
( )
x
, à coor-
denada radial adimensional.
Esse estudo resultou, então, em
relações entre o parâmetro diâme-
tro da partícula e a concentração
de gel, a pressão e a umidade. Na
relação diâmetro da partícula/gel
observou-se que, quanto menor
a partícula, maior a quantidade de
gel formado. Na relação diâmetro/
pressão, verificou-se que a pressão
aumenta conforme se aumenta o
diâmetro da partícula até se atingir
um tamanho crítico, a partir do qual
esse comportamento se inverte, ou
seja, a pressão diminui com o au-
mento do diâmetro. No que se refere
à relação diâmetro/umidade, devido
ao fato da formação do gel consu-
mir água, quanto menor o diâmetro,
menor a umidade relativa dos poros,
pois ocorre a diminuição da absor-
ção de água.
3.3.2 M
odelo
preditivo na
escala
mesoscópica
– D
unant
e
S
crivener
(2010)
O modelo desenvolvido por Du-
nant e Scrivener (2010) demons-
tra a possibilidade de simular os
mecanismos da reação álcali-sílica
baseando-se em uma estrutura de
elementos finitos (AMIE) a qual inte-
gra uma série de ferramentas neces-
sárias para a simulação do concreto.
Nesse modelo, a previsão do dano é
abordada na mesoescala, enquan-
to que a formação do gel na escala
microscópica.
Para a simulação da RAS, os agre-
gados inseridos em uma matriz ci-
mentícia são gerados em uma malha
de elementos finitos, considerando
uma distribuição granulométrica real.
No modelo, ao redor desses agrega-
dos são introduzidas zonas reativas.
A AMIE, então, gera a representação
discreta do arranjo, como ilustrado
pela Figura 6; em cada passo, con-
dições de contorno são aplicadas e
as zonas reativas são expandidas; os
danos causados por essa expansão
são computados e as propriedades
macroscópicas são extraídas. O pro-
cesso, então, repete esses passos
por diversas vezes.
Com a média das tensões e das
deformações em cada ponto da
amostra, pode-se calcular a sua ri-
gidez aparente, e, então, relacionar
o avanço da reação ao nível de dano
na amostra. Esses resultados, en-
tão, são comparados com valores
experimentais. A perda de rigidez é
dada principalmente devido às fis-
suras no agregado e à densidade
u
Figura 6
Representação do modelo - (a) concreto real utilizado na simulação;
(b) simulação em tamanho real; (c) simulação da microestrutura da
argamassa (DUNANT; SCRIVENER, 2010)
7 cm
b
c
a
4 cm


