90 | CONCRETO & Construções
7. CASO DE CARREGAMENTO DE MOMENTOS
CONCENTRADOS NOS APOIOS
7.1 Caso encontrado nas vigas protendidas
pré-tensionadas
A protensão com aderência inicial é obtida em pista de pro-
tensão, na fábrica de peças pré-moldadas; as armaduras de
pretensão são estiradas antes do lançamento do concreto na
forma. Após o endurecimento do concreto, as armaduras são
cortadas, desfazendo-se a ligação com o macaco de protensão.
A força de protensão é transmitida por aderência entre os dois
materiais, pois o concreto impede o encurtamento da armadura.
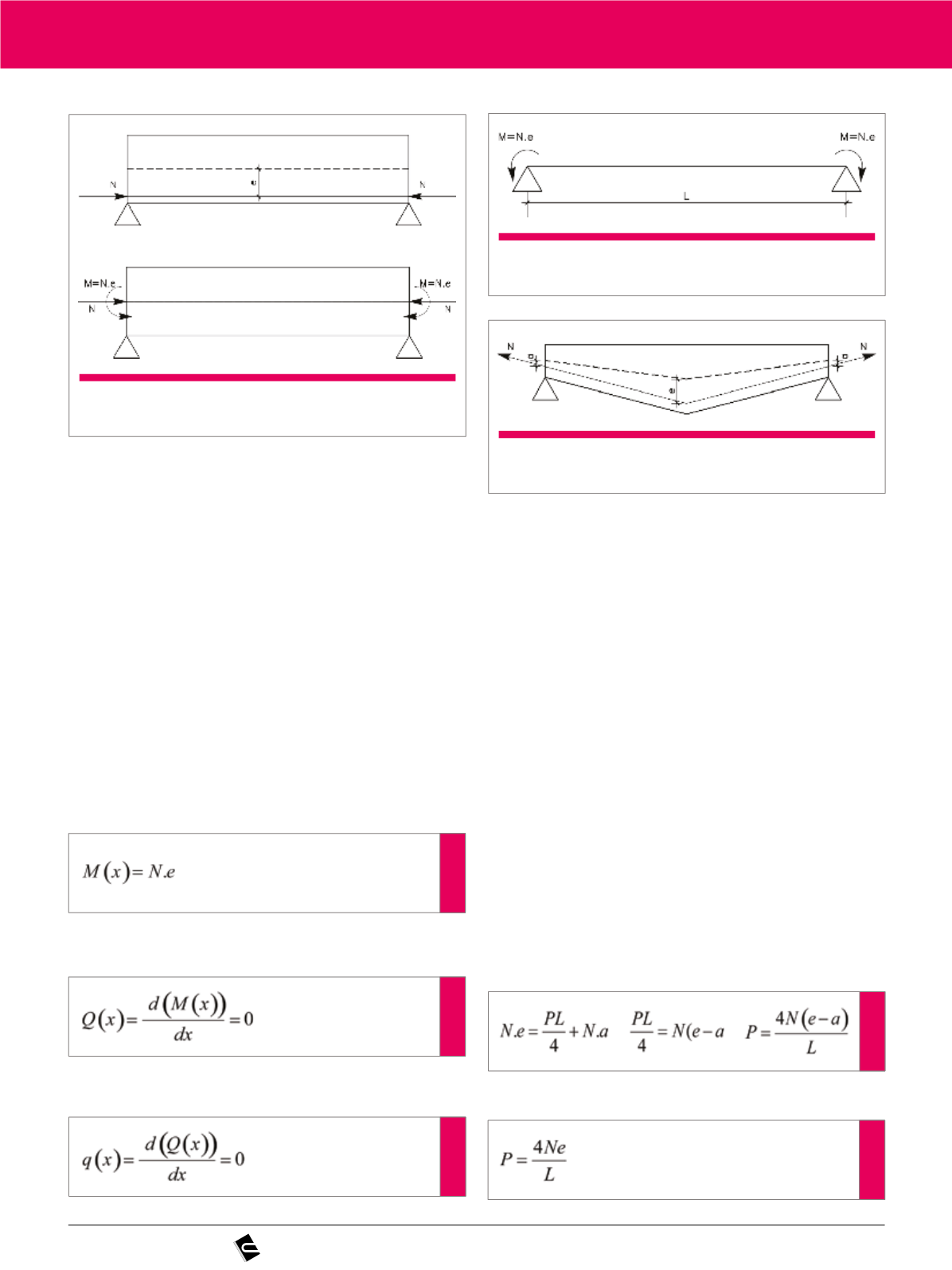
A distribuição dos cabos no interior da viga é visto na figura 5.
A equação do momento fletor da viga da figura 6 é:
[33]
Ao derivar a equação obtida (33), tem-se a equação
do cortante:
[34]
Derivando novamente a equação obtida (34), tem-se a equa-
ção do carregamento:
[35]
Resultando, então, apenas o momento aplicado no extremo
da peça (figura 6).
7.2 Caso de vigas de geometria variável
Outras vigas utilizadas são as de geometria variável. Com
base nas informações obtidas anteriormente, pode-se visualizar
como fica o diagrama de momento fletor das seguintes vigas
(figura 7).
O diagrama de momento de protensão atuante é indutivo e
com forma apresentada na Figura 8.
Logo, podemos analisar e verificar que, em uma viga isostá-
tica, se o diagrama de momentos fletores tem a forma mostrada
na figura 8, então o tipo de carregamento será como mostrado
na figura 9.
Na figura 9, visualiza-se o carregamento “Carga Concentrada“,
mesmo que se tenha um cabo reto, porém com uma viga de inércia
variável. O cabo, mesmo reto, induz o surgimento de uma carga
concentrada devido ao tipo de diagrama momento de protensão
que existe (figura 10). De onde, são extraídas as equações:
[36]
Com
0
a
=
,
[37]
u
Figura 5
Viga isostática de seção constante e cabo reto
u
Figura 6
Momento na extremidade para cabo reto
u
Figura 7
Viga de geometria variável e cabo poligonal


