88 | CONCRETO & Construções
5. CASO DE CARREGAMENTO “CARGA
UNIFORMEMENTE DISTRIBUÍDA“
5.1 No caso de vigas protendidas pós-tensionadas
Na pós-tensão, o cabo é inserido dentro de uma bainha a fim
de impedir o contato com o concreto. Quando o concreto atinge a
resistência desejada, é feito o tensionamento do aço até a tensão de-
sejada com o uso de macacos hidráulicos nas extremidades. Quando
a protensão é introduzida, surge uma força tração nos cabos e, con-
sequentemente, uma tendência desses cabos de se retificar. Como
esses cabos não conseguem se retificar, introduzem na peça de con-
creto um grupo cargas, sejam uniformemente distribuídas, sejam car-
gas concentradas, que, por sua vez, comprimem a peça de concreto.
5.2 Viga isostática de seção constante
e cabo parabólico
Para melhor entendimento, considera-se apenas a carga de pro-
tensão ”N”, desprezando qualquer tipo de perda. De acordo com
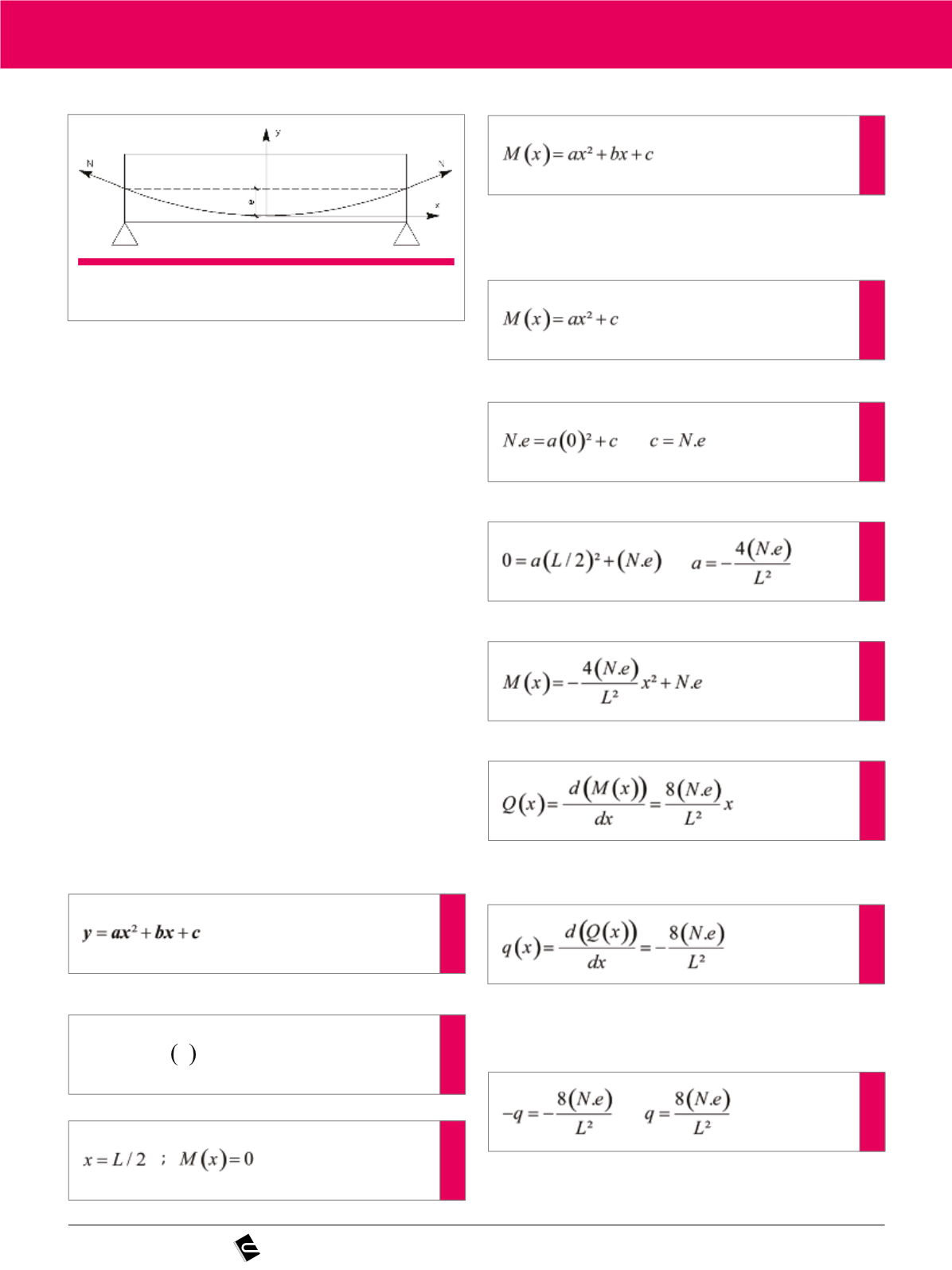
a figura 3, a origem dos eixos no meio do cabo, prova-se a carga
distribuída para estrutura.
A equação do 2º grau relativa à figura 3 é:
[9]
Para:
[10]
0
x
=
;
.
M x N e
=
[11]
[12]
Como a origem dos vértices encontra-se no ponto (0,0), pode-
-se dizer que
0
b
=
!
Então,
[13]
Para
0
x
=
; substituindo (10) em (13):
[14]
Para
/ 2
x L
=
; substituindo (11) e (14) em (13):
[15]
A equação de momento devido à protensão do cabo é:
[16]
Ao derivar a equação obtida (16), tem-se a equação do cortante:
[17]
Derivando novamente a equação obtida (17), tem-se a equação
do carregamento:
[18]
Ou seja, igualando (3) com (18), temos que a protensão
pode ser considerada como um carregamento distribuído
de carga:
[19]
Ou podemos dizer, de uma forma simples e intuitiva, conforme
T.Y. Lin que o momento na seção do ½ do vão é:
u
Figura 3
Cabo parabólico


