CONCRETO & Construções | 87
No final deste trabalho, iremos apresentar as considerações de
simplificação e a possibilidade de utilizar a protensão levando-se em
consideração suas perdas, através das forças de “Desviação“ com-
postas por um conjunto de cargas concentradas ao longo do vão,
de tal forma que, para cada carga concentrada considerada, será
possível calcular a redução da força em cada uma dessas cargas,
pelo efeito de perdas ao longo do comprimento da peça.
4. HIPÓTESES PARA O CÁLCULO
O conceito de resistência dos materiais, no caso de carrega-
mento atuante nas peças, deve ser entendido antes de iniciar o cál-
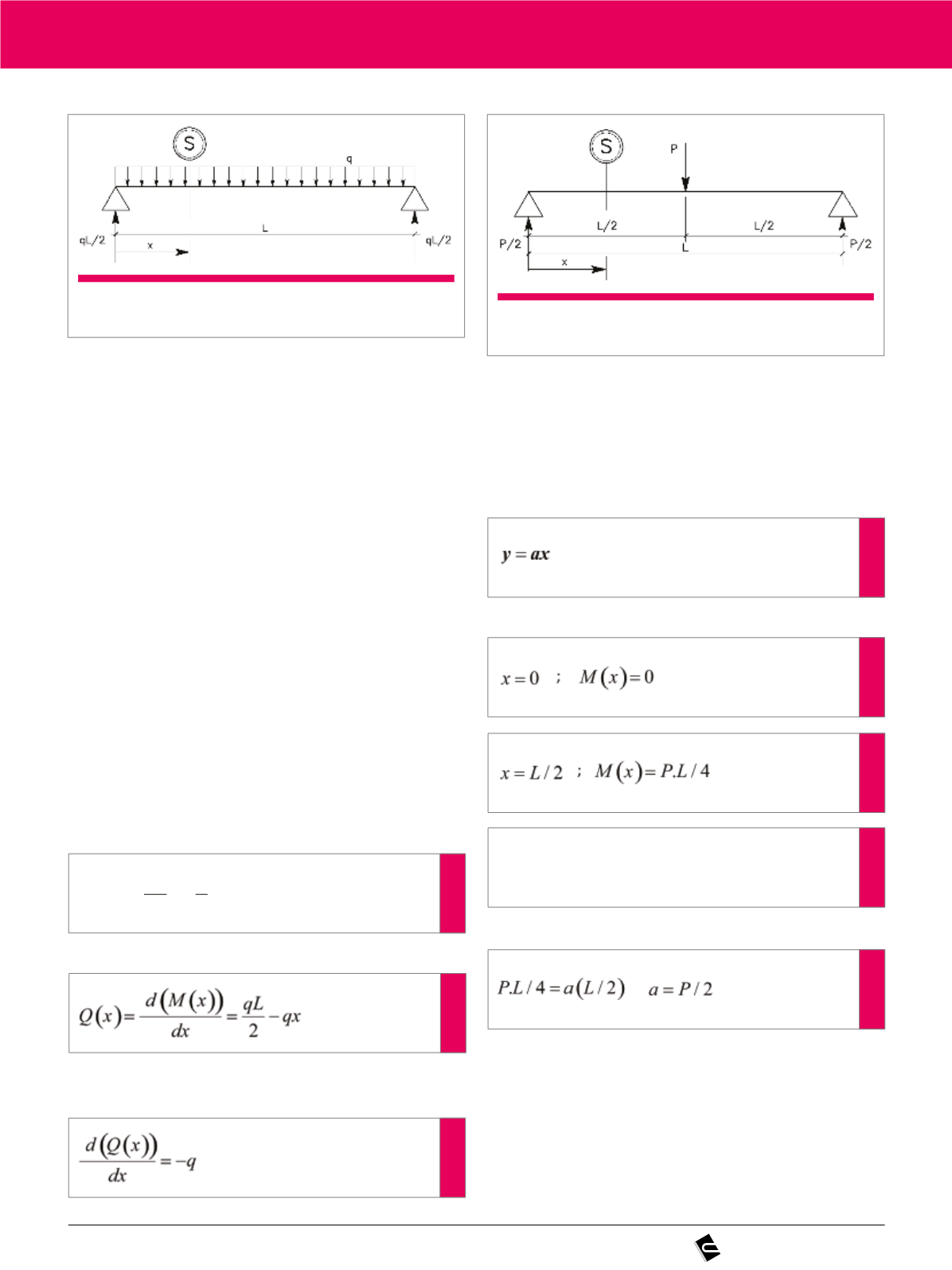
culo da protensão. Portanto, pode-se observar a viga com carga
distribuída “q”; o diagrama de momentos fletores desta parcela varia
em forma de uma parábola. Isso pode ser notado ao calcular o mo-
mento fletor em uma seção qualquer, dada por uma posição x em
relação ao início do vão. No entanto, somente as cargas e reações
à esquerda da seção “S” são contabilizadas. Ou seja, apoio da es-
trutura é substituído pela sua reação e calcula-se na seção “S” os
momentos atuantes oriundos destes carregamentos (figura 1).
A equação do momento fletor da viga da figura 1 é:
[1]
( )
²
22
qL q
M x
x x
= -
Ao derivar a equação obtida (1), tem-se a equação do cortante:
[2]
Derivando novamente a equação obtida (2), tem-se a equação
do carregamento:
[3]
Outro tipo de carregamento a ser estudado é com carga con-
centrada “P”. Neste caso, o diagrama de momento fletor é linear. O
princípio do cálculo do momento fletor é o mesmo do que foi feito
anteriormente para carga distribuída (figura 2).
A equação do 1º grau relativa à figura 2 é:
[4]
Para:
[5]
[6]
[7]
( )
M x ax
=
Para
/ 2
x L
=
; substituindo (6) em (7):
[8]
Visto os casos de carregamentos, inicia-se a protensão in-
troduzida na estrutura, onde o objetivo é diminuir ou até mes-
mo eliminar os esforços de tração aplicados pelo carregamen-
to solicitante. As excentricidades entre o cabo e o centro de
gravidade da viga definem a intensidade desse carregamento.
Contudo, são apresentados exemplos das vigas protendidas
mais usuais.
u
Figura 1
Solicitações no corte S
u
Figura 2
Viga isostática com carga pontual P


