36 | CONCRETO & Construções | Ed. 89 | Jan – Mar • 2018
u
O segmento de parede tem seu
maior vão na vertical e está apoiado
lateralmente, na base e no topo;
u
As tensões geradas pela flexão con-
trolam o dimensionamento;
u
A tensão axial de serviço no ponto
de máximo momento não pode ex-
ceder em 0,04 vezes a resistência
característica do concreto (f
ck
);
u
O momento de fissuração deve ser
menor que o momento resistente de
cálculo (M
n
) minorado de um coefi-
ciente
Φ
, calculado pela Equação 9;
u
A deflexão de serviço, ∆s, não deve
exceder H/150, sendo H a altura li-
vre do painel;
u
Admite-se que as cargas concen-
tradas se espalham verticalmente
em uma razão de 2:1 entre vertical
e horizontal.
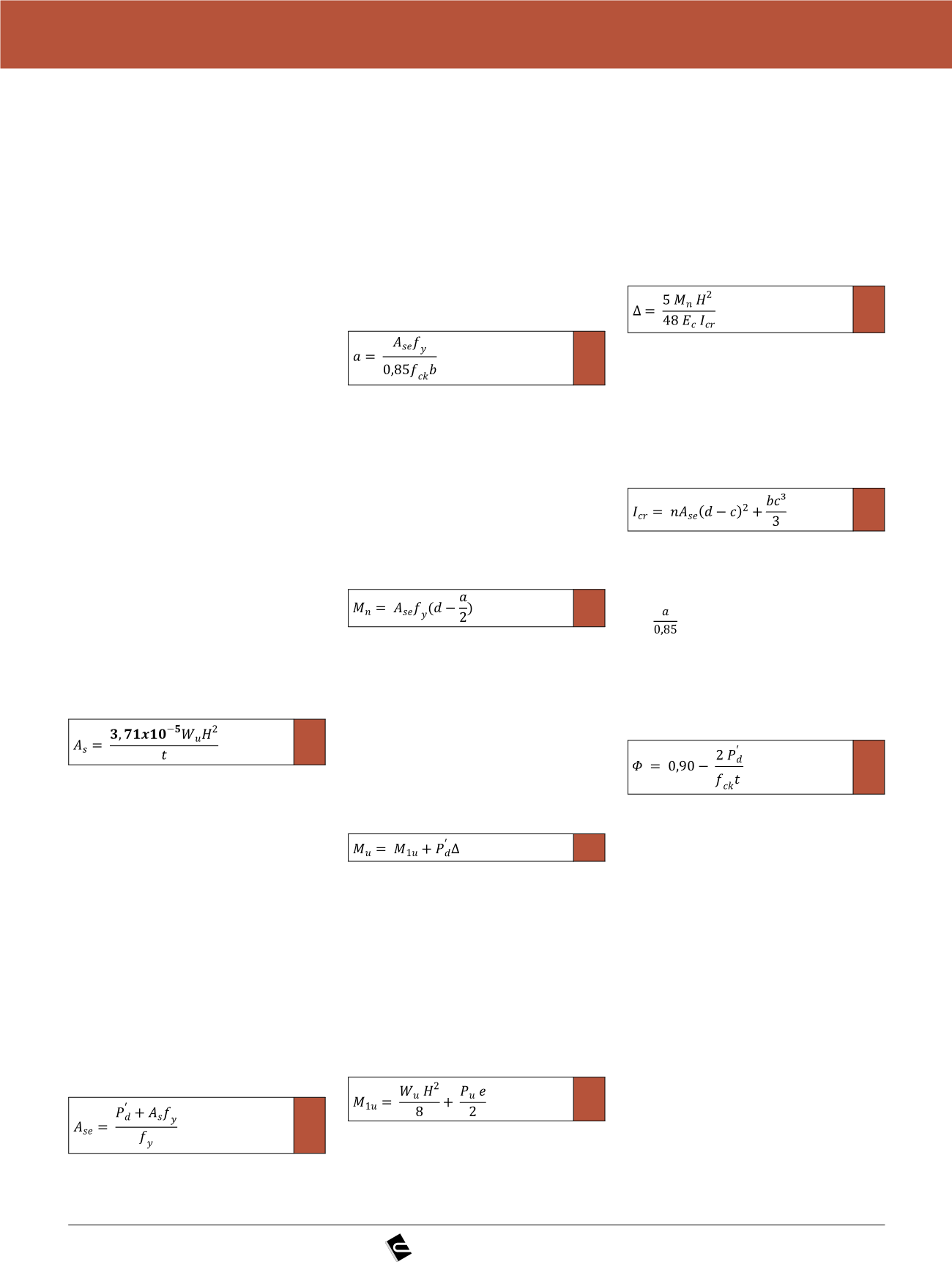
O dimensionamento segundo este
método começa com o cálculo de uma
armadura vertical estimada, A
s
, posi-
cionada no centro da seção do painel,
dada pela Equação 1:
1
Onde:
A
s
= armadura vertical estimada [m²/m]
W
u
= força lateral aplicada sobre a su-
perfície do painel [N/m²];
H = altura livre do painel, em metros;
t = espessura do painel, em metros.
Posteriormente, mantendo-se a al-
tura do painel fixa, calcula-se o momen-
to último resistente da parede para um
metro linear de comprimento de painel.
Primeiro, calcula-se a área efetiva de
armadura que irá resistir às tensões de
tração, A
se
, dada pela Equação 2.
2
Onde:
A
se
= área efetiva de armadura vertical
para um metro de comprimento de pa-
rede [m²];
P
d
’ = força vertical de cálculo aplicada à
meia altura do painel para um metro de
comprimento de parede [N];
f
y
= tensão de escoamento do aço [N/m²].
A altura da linha neutra da seção
de concreto plastificada
a
, é dada pela
Equação 3.
3
Onde:
f
ck
= resistência característica à com-
pressão do concreto [N/m²];
b = largura do segmento de parede em
questão, considerado sempre para a
faixa de um metro.
O momento resistente, M
n
, é dado
pela Equação 4.
4
Onde:
d = distância do centro da armadura à
face comprimida [m].
O momento último de cálculo, M
u
, é
dado pela soma do momento último de
primeira ordem com o momento de se-
gunda ordem, devido ao desvio do eixo
vertical do painel, conforme Equação 5.
5
Onde:
M
1u
= momento último de primeira or-
dem [Nm];
∆ = deflexão do painel à meia altura de-
vido aos efeitos de segunda ordem [m].
O momento último de primeira or-
dem, por sua vez, é estimado por meio
da Equação 6.
6
Onde:
P
u
= carregamento vertical aplicado no
painel [N/m];
e = distância entre o centro do painel e
sua face comprimida [m].
A deflexão do painel à meia altura,
devido aos efeitos de segunda ordem,
pode ser estimada pela Equação 7, que
leva em conta o momento de inércia da
seção fissurada do concreto.
7
Onde:
E
c
= módulo de elasticidade do concre-
to [N/m²];
I
cr
= momento de inércia da seção fissu-
rada do painel de concreto [m
4
], dado
pela Equação 8.
8
Onde:
n = relação entre o módulo de elastici-
dade do aço e do concreto.
c =
O momento último de cálculo, M
u
,
deve ser menor que o momento re-
sistente, M
n
, minorado de um fator
Φ
,
dado pela Equação 9.
9
3. MÉTODO DAS ISOTERMAS DE
500
O
CPARADIMENSIONAMENTO
EM SITUAÇÃO DE INCÊNDIO
A norma ABNT NBR 16475:2017
[9] para o dimensionamento de paredes
de concreto pré-moldado não apresen-
ta uma metodologia para projeto dos
painéis em situação de incêndio. Já, a
norma ABNT NBR 9062:2017 [2], no seu
item 5.3.1.5, apresenta um método para
projeto de painéis maciços de concreto
pré-moldado em situação de incêndio,
que se baseia, unicamente, na especifi-
cação da espessura mínima dos painéis
em função do Tempo Requerido de Re-
sistência ao Fogo (TRRF) da edificação.


