Basic HTML Version
149
IBRACON Structures and Materials Journal • 2012 • vol. 5 • nº 2
D.V. RIBEIRO
| J.A. LABRINCHA
|
M.R. MORELLI
representam a média dos valores obtidos, com seus respectivos
desvios padrões. A concentração de íons cloreto (Cl
-
) aumenta com
o tempo, uma vez que a tensão elétrica é aplicada, forçando estes
íons a migrarem em direção ao pólo positivo do sistema.
Inicialmente, há um período em que a quantidade de cloretos que
passa para a câmara anódica é desprezível. A sua duração cor-
responde ao chamado ‘’time lag’’ (t), e pode ser definido como
o tempo necessário para que os íons cloreto passem através da
amostra de concreto, causando a sua saturação. Este período de
tempo será usado a seguir para estimar os valores de coeficiente
de difusão no estado não estacionário, D
ns
. Após este período, o
fluxo de íons cloreto através da amostra torna-se constante e cor-
responde ao período de estado estacionário.
O “time lag” é empiricamente obtido a partir da interseção entre o
prolongamento da linha que caracteriza o estado estacionário e o
eixo das abscissas (tempo), de acordo com a Figura 5.
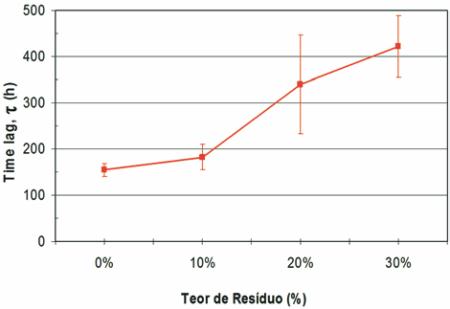
Como pode ser visto na Figura 6, o “time lag” aumenta com o
aumento da adição de lama vermelha, sendo uma provável con-
seqüência da redução da quantidade relativa de poros capilares
[19]. Além disso, as partículas de lama vermelha podem fechar ou
interromper a conectividade entre alguns dos poros, diminuindo
assim a sucção capilar do concreto e, então, impedir o transporte
de substâncias
[20]. Isso acontece mesmo em amostras que apre-
sentaram maior porosidade total, o que significa que, dentro de
certos limites, este parâmetro não é tão relevante.
Após o “time lag”, o fluxo de íons cloreto através da amostra au-
menta a uma taxa constante, correspondendo ao regime de es-
tado estacionário
[16]. A estimativa do coeficiente de difusão no
estado estacionário (D
s
) a partir dos testes de migração é feita
pelo uso da equação de Nernst–Planck modificada:
(1)
DF
=
g
Cl
Cl
S
zFC
RTl
J
D
Sendo: D
s
= coeficiente de difusão no estado estacionário (cm²/s);
J
Cl
= fluxo de íons (mol/(s.cm²)); R = constante de gases (1,9872
cal/(mol.K)); T = temperatura (K); l = espessura do corpo de prova
(cm); z = valência dos íons (para cloretos = 1); F = constante de
Faraday (23063 cal/(volt.eq)); C
Cl
= concentração de íons cloretos
na célula catódica (mol/cm
3
); g = coeficiente de atividade da solu-
ção da célula catódica (0,657 para o Cl
-
); ΔФ = média da tensão
que efetivamente atravessa o corpo de prova durante o estado
estacionário (V).
O fluxo de íons cloreto (J
Cl
) representa a velocidade na qual os
íons são transportados através do concreto e, então, os coeficien-
tes de difusão no estado estacionário e não-estacionário podem
ser calculados. O fluxo de íons cloreto pode ser obtido usando a
inclinação linear do gráfico entre o início e o fim do estado esta-
cionário de difusão e
que representa a evolução da concentração
de cloretos na célula anódica em função do tempo (ver Figura 5).
dt
dC
A
V J
Cl
×
=
Sendo: A= área da seção do corpo de prova exposta (cm²); V = vo-
lume da célula catódica, com cloretos (cm
3
); dC/dt = inclinação da
reta referente ao estado estacionário, no gráfico de concentração
de cloretos versus tempo.
Para calcular o coeficiente de difusão no estado não-estacionário
(D
ns
) a partir de ensaios de migração, faz-se necessário conver-
ter os resultados obtidos a valores equivalentes aos obtidos em
ensaios de difusão natural. O tempo que os íons cloretos teriam
levado para atingir, durante o ensaio de difusão natural, a mesma
profundidade alcançada durante o ensaio de migração acelera-
da, t
dif
, pode ser calculado pelas equações (B) e (C), proposta por
CASTELLOTE et al.
[16].
(2)
úû
ù
êë
é
-
×
×
=
2
2
coth
6 1
2
n
n
tn
dif
t
Figura 6 – Valores de “time lag” ( ),
estimados a partir de ensaios de migração
de cloretos, em função do teor de
lama vermelha adicionado ao concreto
t
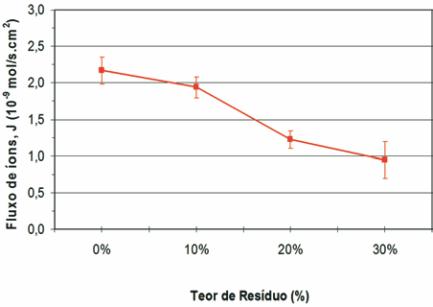
Figura 7 – Fluxo de íons cloreto (J ),
Cl
estimado a partir de ensaios de
migração de cloretos, em função do teor
de lama vermelha adicionado ao concreto

